Probability

The Analysis of Data, volume 1

Basic Definitions: The Probability Functions

1.2. The Probability Function

Definition 1.2.1. Let $\Omega$ be a sample space associated with a random experiment. A probability function $\P$ is a function that assigns real numbers to events $E\subset \Omega$ satisfying the following three axioms.
  1. For all $E$, \[ \P(E)\geq 0.\]
  2. \[\P(\Omega)=1\]
  3. If $E_n, n\in\mathbb{N}$, is a sequence of pairwise disjoint events $(E_i\cap E_j=\emptyset$ whenever $i\neq j)$, then \[ \P\left(\bigcup_{i=1}^{\infty} E_i\right) = \sum_{i=1}^{\infty} \P(E_i).\]

Some basic properties of the probability function appear below.

Proposition 1.2.1. \[\P(\emptyset)=0.\]
Proof. Using the second and third axioms of probability, \begin{align*} 1&=\P(\Omega)=\P(\Omega\cup\emptyset\cup\emptyset\cup\cdots)= \P(\Omega)+\P(\emptyset)+\P(\emptyset)+\cdots\\ &=1+\P(\emptyset)+\P(\emptyset)+\cdots, \end{align*} implying that $\P(\emptyset)=0$ (since $P(E)\geq 0$ for all $E$).
Proposition 1.2.2. (Finite Additivity of Probability). For every finite sequence $E_1,\ldots,E_N$ of pairwise disjoint events ($E_i\cap E_j=\emptyset$ whenever $i\neq j$), \[\P(E_1\cup \cdots \cup E_N)=\P(E_1)+\cdots+\P(E_N).\]
Proof. Setting $E_k=\emptyset$ for $k> N$ in the third axiom of probability, we have \[ \P(E_1\cup \cdots \cup E_N) = \P\left(\bigcup_{i=1}^{\infty} E_i\right) = \sum_{i=1}^{\infty} \P(E_i)=\P(E_1)+\cdots+\P(E_N)+0.\] The last equality above follows from the previous proposition.
Proposition 1.2.3. \[\P(A^c)=1-\P(A).\]
Proof. By finite additivity, \[1=\P(\Omega)=\P(A\cup A^c)=\P(A)+\P(A^c).\]
Proposition 1.2.4. \[\P(A)\leq 1.\]
Proof. The previous proposition implies that $\P(A^c)=1-\P(A)$. Since all probabilities are non-negative $\P(A^c)=1-\P(A)\geq 0$, proving that $\P(A)\leq 1$.
Proposition 1.2.5. If $A\subset B$ then \begin{align*} \P(B)&=\P(A)+\P(B\setminus A)\\ \P(B)&\geq \P(A). \end{align*}
Proof. The first statement follows from finite additivity: \[\P(B)=\P(A\cup (B\setminus A))=\P(A)+\P(B\setminus A).\] The second statement follows from the first statement and the non-negativity of the probability function.
Proposition 1.2.6 (Principle of Inclusion-Exclusion). \[\P(A \cup B)=\P(A)+\P(B)-\P(A\cap B).\]
Proof. Using the previous proposition, we have \begin{align*} \P(A\cup B)&=\P((A\setminus (A\cap B)) \cup (B\setminus (A\cap B)) \cup (A\cap B))\\ &=\P((A\setminus (A\cap B))+\P(B\setminus (A\cap B))) + \P(A\cap B)\\ &=\P(A)-\P(A\cap B)+\P(B)-\P(A\cap B)+\P(A\cap B)\\ &= \P(A)+\P(B)-\P(A\cap B). \end{align*}

Figure 1.2.1 below illustrates the Principle of Inclusion-Exclusion. Intuitively, the probability function $\P(A)$ measures the size of the set $A$ (assuming a suitable definition of size). The size of the set $A$ plus the size of the set $B$ equals the size of the union $A\cup B$ plus the size of the intersection $A\cap B$: $\P(A)+\P(B)=\P(A\cup B)+\P(A\cap B)$ (since the intersection $A\cap B$ is counted twice in $\P(A)+\P(B))$.

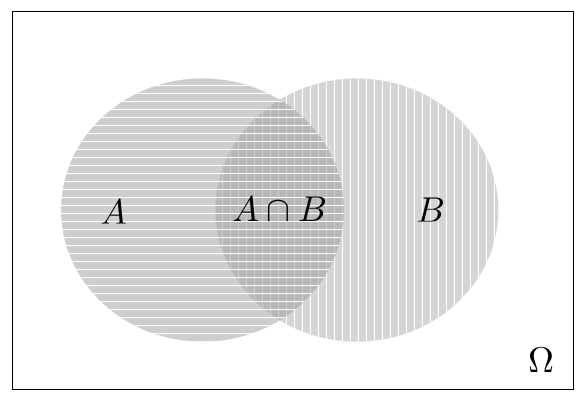
two sets with non-empty intersection

Figure 1.2.1: Two circular sets $A,B$, their intersection $A\cap B$ (gray area with horizontal and vertical lines), and their union $A\cup B$ (gray area with either horizontal or vertical lines or both). The set $\Omega\setminus (A\cup B)=(A\cup B)^c=A^c\cap B^c$ is represented by white color.

Definition 1.2.2 For a finite sample space $\Omega$, an event containing a single element $E=\{\omega\}$, $\omega\in\Omega$ is called an elementary event.

If the sample space is finite $\Omega=\{\omega_1,\ldots,\omega_n\}$, it is relatively straightforward to define probability functions by defining the $n$ probabilities of the elementary events. More specifically, for a sample space with $n$ elements, suppose that we are given a set of $n$ non-negative numbers $\{p_{\omega}: \omega\in\Omega\}$ that sum to one. There exists then a unique probability function $\P$ over events such that $\P(\{\omega\})=p_{\omega}$. This probability is defined for arbitrary events through the finite additivity property \[\P(E)=\sum_{\omega\in E} \P(\{\omega\})=\sum_{\omega\in E} p_{\omega}.\] A similar argument holds for sample spaces that are countably infinite.

The R code below demonstrates such a probability function, defined on $\Omega=\{1,2,3,4\}$ using $p_1=1/2$, $p_2=1/4$, $p_3=p_4=1/8$.

# sample space
Omega = c(1, 2, 3, 4)
# probabilities of 4 elementary events
p = c(1/2, 1/4, 1/8, 1/8)
# make sure they sum to 1
sum(p)

## [1] 1

# define an event 1,4 using a binary
# representation
A = c(1, 0, 0, 1)
# compute probability of A using probabilities of
# elementary events
sum(p[A == 1])

## [1] 0.625