Probability
The Analysis of Data, volume 1
: Differentiation: Univariate Differentiation
$
\def\P{\mathsf{\sf P}}
\def\E{\mathsf{\sf E}}
\def\Var{\mathsf{\sf Var}}
\def\Cov{\mathsf{\sf Cov}}
\def\std{\mathsf{\sf std}}
\def\Cor{\mathsf{\sf Cor}}
\def\R{\mathbb{R}}
\def\c{\,|\,}
\def\bb{\boldsymbol}
\def\diag{\mathsf{\sf diag}}
\def\defeq{\stackrel{\tiny\text{def}}{=}}
$
D.1. Univariate Differentiation
This chapter covers univariate differentiation (differentiation of a function $f:\R\to\R$) and one dimensional Taylor series. It also includes some standard power series results that are used elsewhere in the book. Multivariate differentiation and Taylor series are covered in Chapter F.
Definition D.1.1.
Given a function $f:\R\to\R$, the limit (if it exists)
\[f'(x)=\lim_{t\to x} \frac{f(t)-f(x)}{t-x}\]
is called the derivative of $f$ at $x$. If the derivative exists over a set $A\subset\R$, $f$ is said to be differentiable over that set.
The derivative $f'(x)$ is sometimes denoted $\frac{df(x)}{dx}$ or $df(x)/dx$.
Intuitively, the derivative of a function $f'(x)$ is the slope of the line segment connecting the point $(t,f(t))$ in $\R^2$ to the point $(x,f(x))$ as $t\to x$ (see Figure D.1.1). If $f'(x)$ is positive, the slope is increasing. If $f'(x)$ is negative, the slope is decreasing. The second derivative $f^{(2)}(x)$ is the derivative of the function $f'(x)$: $f^{(2)}(x)=(f')'(x)$. The third and higher derivatives are similarly defined.
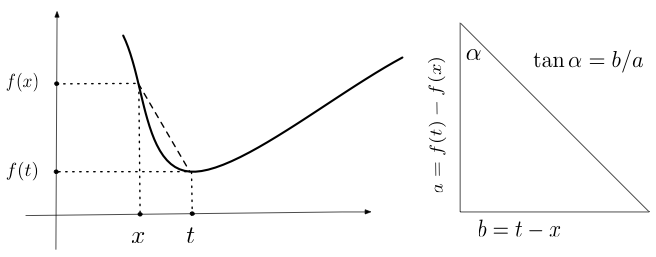
Figure D.1.1: The ratio of $f(t)-f(x)$ to $t-x$ is the slope of the line connecting $(t,f(t))$ and $(x,f(x))$ ($\tan\alpha=b/a$, right panel). The derivative is the limit of that slope $\tan\alpha$ as $t\to x$.
Proposition D.1.2.
If $f$ is differentiable at a point $x$ then it is also continuous at $x$.
Proof.
\[ \lim_{t\to x} f(t)-f(x)=\lim_{t\to x} \frac{f(t)-f(x)}{t-x}(t-x)
= \lim_{t\to x} \frac{f(t)-f(x)}{t-x} \lim_{t\to x}(t-x) = f'(x)\cdot 0=0\]
where the last equality follows from the fact that a product is continuous and continuous functions preserves limits (see Chapter B). It follows that $\lim_{t \to x} f(t) = f(x)$, implying that $f$ is continuous.
Intuitively, a function is differentiable at $x$ when it is smooth rather than having an angle. See Figure D.1.2 for an illustration as well as an example for a function that is continuous but not differentiable (see also Exercise 5 at the end of this chapter).
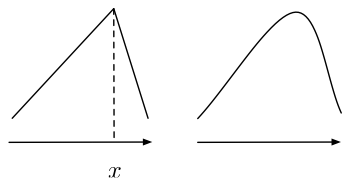
Figure D.1.2: A function is differentiable if it is smooth rather than angular. The function on the right is differentiable everywhere. The function on the left is differentiable everywhere except at the angular position $x$.
Proposition D.1.3.
For two differentiable functions $f,g$ we have
\begin{align*}
(f+g)'(x)&=f'(x)+g'(x)\\
(fg)'(x)&=f'(x)g(x)+f(x)g'(x)\\
(f/g)'(x)&=\frac{g(x)f'(x)-g'(x)f(x)}{g^2(x)}.
\end{align*}
Proof.
The first statement follows from the facts that the ratio in $(f+g)'(x)$ separates into a sum of two ratios and that $\lim f+g=\lim f+\lim g$. The second statement follows form
\begin{align*}
\lim_{t\to x}\frac{f(t)g(t)-f(x)g(x)}{t-x} &= \lim_{t\to x} \frac{f(t)(g(t)-g(x)) + g(x)(f(t)-f(x))}{t-x}\\
&= f(x) \lim_{t\to x}\frac{g(t)-g(x)}{t-x} + g(x) \lim_{t\to x} \frac{f(t)-f(x)}{t-x},
\end{align*}
where we used the fact that $\lim uv=\lim u \cdot \lim v$ and Proposition D.1.1. Similarly, the third statement follows form
\begin{align*}
(f/g)'(x)&=\lim_{t\to x} \frac{1}{g(t)g(x)}\left(g(x)\frac{f(t)-f(x)}{t-x} - f(x)\frac{g(t)-g(x)}{t-x} \right)\\
&=\frac{1}{g^2(x)} \lim_{t\to x} \left(g(x)\frac{f(t)-f(x)}{t-x} - f(x)\frac{g(t)-g(x)}{t-x} \right).
\end{align*}
The derivative of the constant function $f(x)=c$ is zero since the ratio is zero regardless of $t$. The derivative of $f(x)=x$ is 1 since the ratio is always 1 regardless of $t$ (the numerator and denominator cancel out). Repeated applications of the previous proposition shows that $(x^2)'=2x$, $(ax^2)'=2ax$ and by induction $(ax^n)'=a n x^{n-1}$. It follows that every polynomial is differentiable, and its derivative may be obtained by applying the rule $(ax^n)'=a n x^{n-1}$ to each of the polynomial terms separately and adding up the derivatives.
Lemma 3.1.1 (For example (Trench, 2003)).
If $f$ is differentiable at $y_0$ then there exists $r>0$ such that
\[ f(y)=f(y_0)+(f'(y_0)+E(y))(y-y_0), \qquad |y-y_0| < r\]
for some function $E$ that is continuous at $y_0$ and satisfies $E(y_0)=0$.
Proof.
The function
\begin{align*}
E(y)= \begin{cases} 0 & y=y_0\\ \frac{f(y)-f(y_0)}{y-y_0} - f'(y_0) & y\neq y_0\end{cases}
\end{align*}
is continuous at $y=y_0$ and satisfies the statement in the proposition.
Lemma 3.1.1 (Chain Rule).
For two differentiable function $f,g:\R\to\R$
\[(f\circ g)'(x_0)=f'(g(x_0))g'(x_0).\]
Proof.
\begin{align*}
\lim_{x\to x_0} \frac{f(g(x))-f(g(x_0))}{x-x_0}&=\lim_{x\to x_0} \frac{(f'(g(x_0))+E(g(x)))(g(x)-g(x_0))}{x-x_0} \\ &= f'(g(x_0))g'(x_0)
\end{align*}
where we used Lemma D.1.1 in the first equality (applied $f$ and $y_0=g(x_0)$), the continuity of $g$ and of $E$ at $g(x_0)$, and $E(g(x_0))=0$ in the second equality.
Definition D.1.2.
A function $f:A\subset\R\to\R$ has a local maximum at $x\in A$ if $f(x)$ is higher or equal than all values in $\{f(y):y\in B_r(x)\}$ for some $r > 0$. A function $f:A\subset\R\to\R$ has a local minimum at $x\in A$ if $f(x)$ is lower or equal than all values in $\{f(y):y\in B_r(x)\}$ for some $r > 0$.
Proposition D.1.4.
If a differentiable function $f:[a,b]\to\R$ has a local maximum or a local minimum at $x\in(a,b)$, then $f'(x)=0$.
Proof.
Assume $f$ has a local maximum at $x$ and $f(x)$ is greater or equal than all values $f(y)$ where $|y-x| < r$ for some $r > 0$. Setting $\delta=r$, if $x-\delta < y < x$ then $(f(y)-f(x))/(y-x)\geq 0$, implying that $f'(x)\geq 0$. Similarly if $x < y < x+\delta$, then $(f(y)-f(x))/(y-x)\leq 0$, implying that $f'(x)\leq 0$. We conclude that $f'(x)=0$. A similar proof applies to the local minimum case.
Proposition D.1.4 (Mean Value Theorem).
For any two differentiable functions $f,g:[a,b]\to\R$ there exists a point $x\in (a,b)$ such that
\[ (f(b)-f(a)) g'(x) = (g(b)-g(a)) f'(x).\]
In particular, setting $g(x)=x$ we get that there exists a point $x\in (a,b)$ such that
\[f'(x)=\frac{f(b)-f(a)}{b-a}.\]
Proof.
The function \[h(x)=(f(b)-f(a))g(x)-(g(b)-g(a))f(x)\] is continuous, differentiable, and satisfies \[h(a)=f(b)g(a)-f(a)g(b)=h(b).\] Since $[a,b]$ is compact, by Proposition B.3.6, $h$ attains its maximum and minimum on $[a,b]$.
Since $h(a)=h(b)=0$, if $\max_{x\in [a,b]} h(x) \neq 0$, the maximum occurs in $(a,b)$ and by Proposition D.1.4 $h'(x)=0$. Similarly, if $\max_{x\in [a,b]} h(x) \neq 0$, then $h'(x)=0$ as well. If both the minimum and maximum are 0 then $h(y)$ equals 0 for all $y$, and in particular $h'(x)=0$.
Proposition D.1.6.
For a differentiable function $f:(a,b)\to\R$, we have
- If $f'(x)\geq 0$ for all $x\in (a,b)$ then $f$ is monotonic increasing,
- if $f'(x)\leq 0$ for all $x\in (a,b)$ then $f$ is monotonic decreasing,
- if $f'(x) > 0$ for all $x\in (a,b)$ then $f$ is strictly monotonic increasing,
- if $f'(x) < 0$ for all $x\in (a,b)$ then $f$ is strictly monotonic decreasing,
- if $f'(x) = 0$ for all $x\in (a,b)$ then $f$ is constant,
Proof.
The mean-value theorem above implies that for all $(u,v)\subset(a,b)$ there exists $x\in (u,v)$ such that
\[ f(v)-f(u)=(v-u)f'(x)\geq 0.\]
The rest of the proof is similar.
In many cases it is easy to find the limit of a ratio $\lim (f(x)/g(x))$ using Proposition B.4.8 that implies $\lim (f(x)/g(x))=(\lim f(x))/(\lim g(x))$, assuming that the (a) denominator is not zero, and (b) the numerator and denominator are finite. For example,
\[ \lim_{x\to 0} \frac{x^2+4x}{\cos x}=\frac{\lim_{x\to 0} x^2+4x}{\lim_{x\to 0} \cos x} =\frac{0}{1}=0.\]
L'Hospital's rule below may be used to compute $\lim f(x)/g(x)$ when either (a) or (b) fails.
Proposition D.1.7 (L'Hospital's Rule)
For two differentiable functions $f,g:[\alpha,\beta]\to\R$, if
\[(a): \qquad \lim_{x\to a}f(x)=0 =\lim_{x\to a} g(x)\]
or
\[(b): \qquad \lim_{x\to a}f(x)=\pm \infty=\lim_{x\to a} g(x)\]
(where the value $a$ may be finite, $\infty$, or $-\infty$) then
\[ \lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f'(x)}{g'(x)},\]
assuming that the limit in the right hand side above exists.
Proof.
We assume that $f',g'$ are continuous and $\lim_{x\to a}f(x)=\lim_{x\to a} g(x)= 0$ (condition (a)). In this case $f(a)=g(a)=0$ and
\begin{align*}
\lim_{x\to a}\frac{f(x)}{g(x)} &= \lim_{x\to a} \frac{\frac{f(x)-f(a)}{x-a}}{\frac{g(x)-g(a)}{x-a}} =
\frac{\lim_{x\to a}\frac{f(x)-f(a)}{x-a}}{\lim_{x\to a}\frac{g(x)-g(a)}{x-a}} = \frac{f'(a)}{g'(a)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}.
\end{align*}
A similar proof applies if condition (b) holds. Proofs without requiring continuity of $f',g'$ appear in (Rudin, 1976) or (Trench, 2003).
Example D.1.1.
We have
\[ \lim_{x\to 0} \frac{x^2+4x}{\sin x}=\frac{\lim_{x\to 0} (x^2+4x)'}{\lim_{x\to 0} (\sin x)'} =\frac{\lim_{x\to 0} 2x+4}{\lim_{x\to 0} \cos x}=\frac{4}{1}.\]
Note that an application of the ratio rule $\lim (u/v)=\lim u / \lim v$ does not work here since the limit of the numerator and the limit of the denominator both equal 0.

