Probability

The Analysis of Data, volume 1

Law of Large Numbers

8.6. Law of Large Numbers

Proposition 8.6.1 (Markov Inequality). \[\P(|X|\geq \alpha) \leq \frac{\E(|X|^k)}{\alpha^k}, \qquad \forall \alpha>0,\quad \forall k\in\mathbb{N}.\]
Proof. If $X$ is continuous, \begin{align*} \E(|X|^k) &=\int_{-\infty}^{\infty}|x|^k f_X(x)dx =\int_{0}^{\infty} |x|^k f_X(x)dx \\ &\geq \int_{\alpha}^{\infty}|x|^k f_X(x)dx \geq \int_{a}^{\infty} a^k f_X(x)dx = \alpha^k \P(|X|\geq a). \end{align*} If $X$ is discrete, replace the integrals above with sums. The general case follows from Lebesgue integration theory.
Corollary 8.6.1 (Chebyshev Inequality). \[\P(|X-E(X)|\geq \alpha)\leq \frac{\Var(X)}{\alpha^2}, \qquad \forall \alpha>0.\]
Proof. Apply Markov inequality $\P(Z^2\geq \alpha^2)\leq \E(Z^2)/\alpha^2$ to the RV $Z^2$ where $Z=|X-E(X)|$. This gives \[\P(|X-E(X)|\geq \alpha)=\P(Z\geq \alpha)=\P(Z^2\geq \alpha^2)\leq \frac{\Var(X)}{\alpha^2}.\]
Proposition 8.6.2 (Strong Law of Large Numbers). For a sequence of iid random vectors $\bb{X}^{(n)}, n\in\mathbb{N}$ with finite fourth moments ($\E({{\bb X}^{(1)}}^4) < \infty$), \[\frac{1}{n}\sum_{i=1}^n\bb{X}^{(i)} \tooas \E({\bb X}^{(1)}).\]
Proof. Convergence with probability 1 of the $d$-dimensional sequence of RV occurs if and only if each of the components converge to the corresponding limit. It follows that it is sufficient to prove the above theorem in the scalar case.

Applying Cauchy-Schwartz inequality (Proposition B.4.1) to the inner product $g(X^2,1)=\E(X^2\cdot 1)$ we have that $\E(X^2)^2\leq \E(X^4)$. Similarly, we have $\E(X)^2\leq \E(X^2)$. This shows that $\E(X^r), 1\leq r\leq 4$ is finite if $\E(X^4) < \infty$.

We assume below that $\E(X^{(1)})=0$. We can then prove the general case by applying the obtained result to the sequence $Y^{(n)}=X^{(n)}-\E(X^{(1)})$: $n^{-1}\sum Y^{(n)}\tooas 0$, which implies $n^{-1}\sum X^{(n)}\tooas \E(X^{(1)})$.

We have \begin{align*} \E\left((\sum_{i=1}^n X^{(i)})^4\right) &= \E\left(\sum_{i=1}^n (X^{(i)})^4+6 \sum_{1\leq i < j\leq n} (X^{(i)})^2(X^{(i)})^2\right). \end{align*} The missing terms in the sum above are either $\E(X^{(i)}X^{(j)}X^{(k)}X^{(l)})$ for distinct $i,j,k,l$ or $\E((X^{(i)})^3 X^{(j)})$ for distinct $i,j$. In either case, these terms are zero since expectation of a product of independent RVs is a product of the corresponding expectation, and since $\E(X^{(i)})=0$. The reason for the coefficient 6 is that if we fix the index of the first term in $X^{(a)}X^{(b)}X^{(c)}X^{(d)}$ to be $a=i$, there are three remaining variables that can receive the same index $i$ (the remaining indices get the value $j$). Alternatively, the index of the first variable may be $j$, yielding 3 more terms with the required multiplicity of indices.

This leads to the bound \begin{align*} \E\left(\left(\sum_{i=1}^n X^{(i)}\right)^4\right) &\leq n M + 6 \begin{pmatrix}n\\2\end{pmatrix} M' = nM+3n(n-1)M' \leq n^2 M'' \end{align*} for some finite $M,M',M''<\infty$. Applying Markov's inequality with $k=4$, we get \begin{align*} \P\left(\Big|n^{-1}\sum_{i=1}^n X^{(i)})\Big| \geq \epsilon \right ) = \P\left(\Big|\sum_{i=1}^n X^{(i)})\Big| \geq n \epsilon \right ) \leq M n^{-2}\epsilon^{-4}, \end{align*} which combined with the first Borell-Cantelli lemma (Proposition 6.6.1) shows that \[\P\left(\Big|n^{-1}\sum_{i=1}^n X^{(i)})\Big| \geq \epsilon \text{ i.o.} \right )=0.\] Proposition 8.2.1 completes the proof.

The proposition above remains true under the weaker condition of finite first moment $\E({\bb X}^{(1)}) < \infty$. The proof, however, is considerably more complicated in this case (Billingsley, 1995).

Corollary 8.6.2 (Weak Law of Large Numbers). For a sequence of iid random vectors $\bb{X}^{(n)}, n\in\mathbb{N}$ with finite fourth moment $\E({{\bb X}^{(1)}}^4) < \infty$, \[\frac{1}{n}\sum_{i=1}^n\bb{X}^{(i)} \toop \E({\bb X}^{(1)}).\]
Proof. This follows from the strong law of large numbers and Corollary 8.2.1.

The weak law of large numbers (WLLN) shows that the sequence of random vectors $\bb{Y}^{(n)}=\frac{1}{n}\sum_{i=1}^n\bb{X}^{(i)}$, $n=1,2,\ldots$ is increasingly similar in values to the expectation vector $\bb \mu$. Thus for large $n$, $\bb{Y}^{(n)}$ may be intuitively considered as a deterministic RV whose value is $\mu$ with high probability.

An important special case occurs when $X^{(i)}$ are iid indicator variables $X^{(i)}(\omega)=I_A(\omega)$ with respect to some set $A\subset\R$. In this case, the average $\frac{1}{n}\sum_{i=1}^n\bb{X}^{(i)}=\frac{1}{n}\sum_{i=1}^n I_A$ becomes the relative frequency of occurrence in the set $A$ and the expectation $\E(X^{(i)})$ becomes $\E(I_A)=\P(A)$. We thus have a convergence of relative frequencies as $n\to\infty$ to their expectation.

We demonstrate the WLLN below by drawing samples $X^{(n)}$, $i=1,\ldots,n$ iid from a uniform distribution over $\{1,\ldots,6\}$ (fair die) and displaying $X^{(n)}$ together with the averages $Y^{(n)}=\sum_{i=1}^n X^{(n)}/n$ for different $n$ values.

# draw 10 samples from U({1,...,6})
S = sample(1:6, 10, replace = TRUE)
S

##  [1] 2 3 4 6 2 6 6 4 4 1

# compute running averages of 1,...,10 samples
cumsum(S)/1:10

##  [1] 2.000 2.500 3.000 3.750 3.400 3.833 4.143
##  [8] 4.125 4.111 3.800

The example above shows that as $n$ increases, the averages get closer and closer to the expectation 3.5. Below is a graph for larger $n$ values. Note how the variations around 3.5 diminish for large $n$. 

S = seq(from = 1, to = 6, length = 200)
par(cex.main = 1.5, cex.axis = 1.2, cex.lab = 1.5)
plot(1:200, S, type = "n", xlab = "$n$", ylab = "$(X_1+\\cdots+X_n)/n$")
for (s in 1:100) lines(1:200, cumsum(sample(1:6, 200,
    replace = TRUE))/1:200, col = rgb(0, 0, 0, alpha = 0.3))

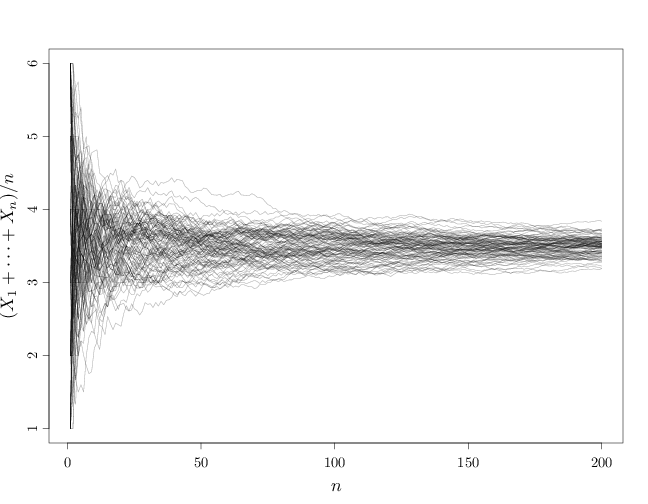
This is one instantiation of the sequence of die rolls. Other instantiations will produce other graphs. The WLLN states that all such graphs will become arbitrarily close to 3.5 as $n$ increases.