Probability
The Analysis of Data, volume 1
The Lebesgue Integral*
$
\def\P{\mathsf{\sf P}}
\def\E{\mathsf{\sf E}}
\def\Var{\mathsf{\sf Var}}
\def\Cov{\mathsf{\sf Cov}}
\def\std{\mathsf{\sf std}}
\def\Cor{\mathsf{\sf Cor}}
\def\R{\mathbb{R}}
\def\c{\,|\,}
\def\bb{\boldsymbol}
\def\diag{\mathsf{\sf diag}}
\def\defeq{\stackrel{\tiny\text{def}}{=}}
$
F.3. The Lebesgue Integral*
In the definitions and propositions below, we assume the presence of a measure space $(\Omega,\mathcal{F},\mu)$ ($\Omega$ is an arbitrary set, $\mathcal{F}$ is a $\sigma$-algebra on $\Omega$, and $\mu$ is a measure $\mu:\mathcal{F}\to\R$). We assume below and in the rest of this book that $0\cdot \infty=0$.
Definition F.3.1.
A function $f:\Omega\to\R$ is simple if it has finite range, or in other words we can write $f$ as
\[ f(\omega) = \sum_{i=1}^n c_i I_{A_i}(\omega),\quad n\in\mathbb{N}, \quad c_i\in\R\]
for some sets $A_i\subset\Omega$, $i=1,\ldots,n$ ($I_A(\omega)=1$ if $\omega\in A$ and 0 otherwise).
Proposition F.1.1.
If $f:\Omega\to\R$ is a measurable function, then there exists a sequence of simple measurable functions $f_n:\Omega\to\R, n\in\mathbb{N}$ such that
\begin{align*}
f(\omega)\geq 0 & \qquad \text{implies} \qquad 0 \leq f_n(\omega)\nearrow f(\omega)\\
f(\omega)\leq 0 & \qquad \text{implies} \qquad 0 \geq f_n(\omega)\searrow f(\omega).
\end{align*}
(Recall Definition B.2.12 regarding the notations $\nearrow,\searrow$.)
Proof.
The sequence of functions
\begin{align*}
f_n(\omega) =
\begin{cases}
-n & -\infty \leq f(\omega)\leq -n\\
-(k-1)2^{-n} & -k 2^{-n}< f(\omega)\leq -(k-1)2^{-n}, \quad 1\leq k\leq n2^n\\
(k-1)2^{-n} & (k-1)2^{-n}\leq f(\omega) < k 2^{-n}, \quad 1\leq k \leq n2^n\\
n & n\leq f(\omega)\leq +\infty
\end{cases}
\end{align*}
has the necessary properties (see the following example for an illustration).
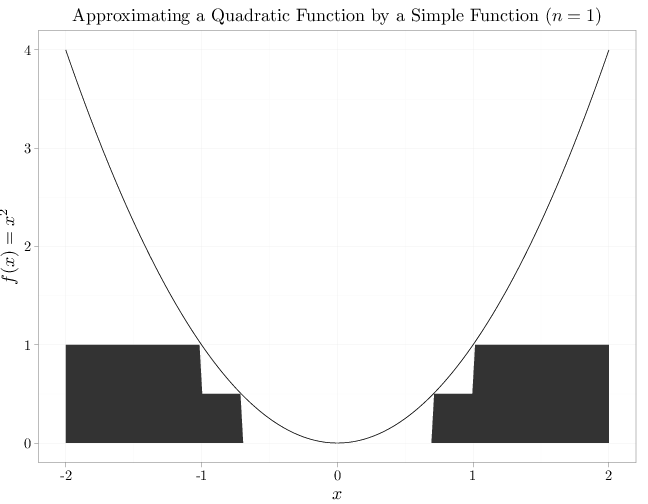
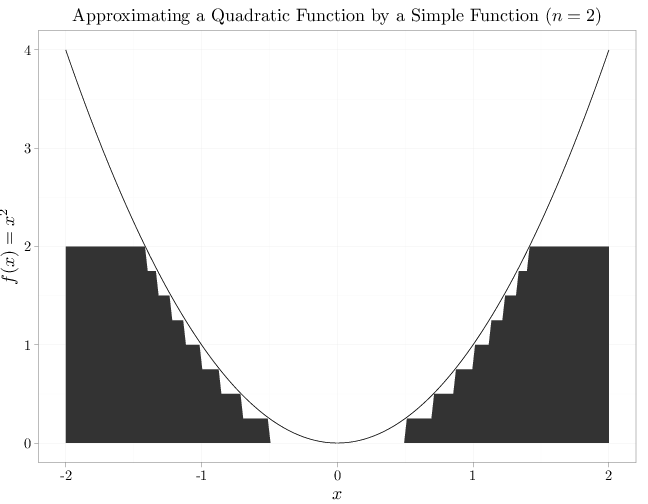
Example F.3.1.
In the case of $f(x)=x^2$, the functions $f_1$ and $f_2$ in the proof of the above proposition are
\begin{align*}
f_1(\omega) &=
\begin{cases}
0 & 0 \leq f(\omega) < 1/2\\
1/2 & 1/2 \leq f(\omega) < 1\\
1 & 1\leq f(\omega)\leq +\infty
\end{cases},\\
f_2(\omega) &=
\begin{cases}
0 & 0 \leq f(\omega) < 1/4\\
1/4 & 1/4 \leq f(\omega) < 2/4\\
2/4 & 2/4 \leq f(\omega) < 3/4\\
3/4 & 3/4 \leq f(\omega) < 4/4\\
4/4 & 4/4 \leq f(\omega) < 5/4\\
5/4 & 5/4 \leq f(\omega) < 6/4\\
6/4 & 6/4 \leq f(\omega) < 7/4\\
7/4 & 7/4 \leq f(\omega) < 8/4\\
2 & 2\leq f(\omega)\leq +\infty
\end{cases}.
\end{align*}
The figures below illustrate these functions in the case of $\Omega=\R$.
X = seq(-2, 2, length.out = 200)
f1 = rep(0, length.out = 200)
f1[X^2 > 1/2 & X^2 < 1] = 1/2
f1[X^2 > 1] = 1
qplot(X, X^2, xlab = "$x$", ylab = "$f(x)=x^2$", geom = "line",
main = "Approximating a Quadratic Function by a Simple Function ($n=1$)") +
geom_area(aes(x = X, y = f1))
f2 = rep(0, length.out = 200)
f2[X^2 > 1/4 & X^2 < 2/4] = 1/4
f2[X^2 > 2/4 & X^2 < 3/4] = 2/4
f2[X^2 > 3/4 & X^2 < 4/4] = 3/4
f2[X^2 > 4/4 & X^2 < 5/4] = 4/4
f2[X^2 > 5/4 & X^2 < 6/4] = 5/4
f2[X^2 > 6/4 & X^2 < 7/4] = 6/4
f2[X^2 > 7/4 & X^2 < 8/4] = 7/4
f2[X^2 > 8/4] = 2
qplot(X, X^2, xlab = "$x$", ylab = "$f(x)=x^2$", geom = "line",
main = "Approximating a Quadratic Function by a Simple Function ($n=2$)") +
geom_area(aes(x = X, y = f2))
Definition F.3.2.
The Lebesgue integral of a non-negative measurable simple function is
\[ \int_E \sum_{i=1}^n \alpha_i I_{A_i}\, d\mu
\defeq \sum_{i=1}^n \alpha_i\, \mu(A_i\cap E), \qquad E\in\mathcal{F}.\]
Definition F.3.3.
The Lebesgue integral of a non-negative measurable function is
\[ \int_E f \, d\mu \defeq \sup_g \int_E g\, d\mu, \qquad E\in\mathcal{F},\]
where the supremum ranges over all simple measurable functions $g$ such that $0\leq g\leq f$.
Note that if $f$ is a non-negative measurable simple function, there are two possible definitions for $\int_E f\,d\mu$ (Definition F.3.2 and Definition F.3.3). Fortunately, they both agree as the supremum in the Definition F.3.3 is realized by $g=f$.
Proposition F.3.2.
Let $f$ be a non-negative measurable function $f$.
- If $f\leq g$ then $\int_E f\, d\mu \leq \int_E g\, d\mu$.
- If $A\subset B$ then $\int_A f\,d\mu \leq \int_B f\,d\mu$.
- If $c\in [0,\infty)$ then $\int_E cf\,d\mu = c\int_E f\,d\mu$.
- If $f(x)=0$ for all $x\in E$ then $\int_E f\, d\mu=0$.
- If $\mu(E)=0$ then $\int_E f\, d\mu=0$.
- $\int_E f\,d\mu = \int_{\Omega} (I_E f) \, d\mu$.
Proof.
These properties follow directly from Definitions F.3.2-F.3.3. The first property follows from the fact that the supremum in the definition of $\int_E f\, d\mu$ is less than or equal to the supremum in the definition of $\int_E g\, d\mu$. The second property holds since the supremum in the definition of $\int_A f\,d\mu$ is less than or equal than the supremum in the definition of $\int_B f\,d\mu$. The third property follows from the fact that the supremum in the definition of $\int_E cf\,d\mu$ is $c$ times the supremum in the definition of $\int_E f\,d\mu$. The fourth property follows from the fact that the supremum in the definition of $\int_E f\,d\mu$ can only be the zero function. The fifth property follows since the integrals of all simple functions over $E$ are zero. The sixth property follows directly from Definitions F.3.2-F.3.3.
Proposition F.3.3.
Let $(\Omega,\mathcal{F},\mu)$ be a measure space. For two non-negative measurable simple functions $s,t:\Omega\to[0,\infty]$, we have
\[ \int_{\Omega} (s+t)\, d\mu = \int_{\Omega} s\, d\mu + \int_{\Omega} t\, d\mu\]
and $\phi(E)=\int_E s\,d\mu$ is a measure function on $(\Omega,\mathcal{F})$.
Proof.
We assume that $s=\sum_{i=1}^k \alpha_i I_{A_i}$ and $t=\sum_{i=1}^l \beta_i I_{B_i}$. For all sets $E\in\mathcal{F}$, we have $\phi(E)\geq 0$ and $\phi(\emptyset)=0$. If $E_n, n\in\mathbb{N}$ is a sequence disjoint sets in $\mathcal{F}$ with $\cup_n E_n=E$ then
\begin{align*}
\phi(E) &= \int_E \sum_{i=1}^k \alpha_i I_{A_i}\, d\mu = \sum_{i=1}^k \alpha_i \mu(A_i\cap E) = \sum_{i=1}^k \sum_{n\in\mathbb{N}}\alpha_i \mu(A_i\cap E_n)\\
&= \sum_{n\in\mathbb{N}} \phi(E_n),
\end{align*}
proving that $\phi$ is a measure.
For all $E_{ij}=A_i\cap B_j$, $i=1,\ldots,k$, $j=1,\ldots,l$
\begin{align*}
\int_{E_{ij}} (s+t)\, d\mu = (\alpha_i+\beta_j) \mu(E_{ij}) =
\int_{E_{ij}} s\, d\mu + \int_{E_{ij}} t\, d\mu.
\end{align*}
Since $\phi$ is a measure, it is countable additive and so the above equation implies $\int_{\Omega} (s+t)\, d\mu =
\int_{\Omega} s\, d\mu + \int_{\Omega} t\, d\mu.$
Proposition F.3.4 (Monotone Convergence Theorem).
\[ 0\leq f_n\nearrow f \quad \text{implies} \quad
\int_{\Omega} f_n\, d\mu \nearrow \int_{\Omega} f \, d\mu.\]
Proof.
The function $f=\lim f_n$ is measurable by Proposition E.6.4, and since $\int f_n\,d\mu \nearrow$, we have $\int f_n\,d\mu\nearrow \alpha$ for some $\alpha\in[0,+\infty]$ (see Proposition B.2.1). Since $f_n \leq \lim f_n$, we have $\int f_n\,d\mu \leq \int_{\Omega} \lim_{n\to\infty} f_n \, d\mu$.
It remains to show the reverse inequality $\int f_n\,d\mu \geq \int_{\Omega} \lim_{n\to\infty} f_n \, d\mu$. For any non-negative simple measurable function $s$ such that $s\leq \lim f_n$ and any $c\in (0,1)$ we define $E_n=\{x:f_n(x)\geq cs(x)\}, n\in\mathbb{N}$. Note that $E_n\in\mathcal{F}$, $E_n\nearrow$, and $\Omega=\cup_n E_n$. By definition of $E_n$, we have for all $n\in\mathbb{N}$
\begin{align}
\int_{\Omega} f_n \, d\mu \geq \int_{E_n} f_n\,d\mu \geq c\int_{E_n} s\, d\mu.
\end{align}
We let $n\to\infty$ and recall that $\int_{E_n} s\, d\mu$ is a measure (Proposition F.3.3) $\phi(E_n)$, which converges by Proposition E.2.1 to $\phi(\Omega)$. This implies that
\[\lim \int_{\Omega} f_n \, d\mu \geq \lim c\int_{E_n} s\, d\mu = c \int_{\Omega} s\, d\mu.\]
Since this holds for any $c\in (0,1)$ we also have
\[\lim \int_{\Omega} f_n \, d\mu \geq \int_{\Omega} s\, d\mu.\]
Finally, since this holds for all non-negative simple measurable function $s$ such that $s\leq \lim f_n$, it also holds for their supremum, which defines the integral $\int_{\Omega} \lim f_n\, d\mu$.
Corollary F.3.1.
Let $f_n, n\in\mathbb{N}$ be a sequence of non-negative measurable functions whose sum $\sum_{n=1}^{\infty} f_n(x)$ converges for all $x$. Then
\[ \int_{\Omega} \sum_{n=1}^{\infty} f_n\, d\mu \,\, =\,\, \sum_{n=1}^{\infty} \int_{\Omega} f_n\, d\mu.\]
Proof.
We first prove this result for a sum of two functions $f_1+f_2$. Let $s_k$ and $t_k$ be the sequence of measurable functions that converge to $f_1$ and $f_2$ as in Proposition F.3.1. Then the sequence of simple functions $s_k+t_k$ converge to $f_1+f_2$, and using the Monotone Convergence Theorem above together with Proposition F.3.3, we have
\begin{align*}
\int_{\Omega} f_1+f_2\,d\mu &= \int_{\Omega} \lim_k (s_k+t_k)\,d\mu
= \lim_k \int_{\Omega} s_k+ t_k \,d\mu\\
&=\lim_k \int_{\Omega} s_k\, d\mu + \lim_k \int_{\Omega} t_k \,d\mu
= \int_{\Omega} f_1\,d\mu + \int_{\Omega} f_2\,d\mu.
\end{align*}
By induction, we establish the result for a sum of $N$ functions.
Defining $g_N=\sum_{n=1}^N f_n$, we have that $g_N\nearrow \sum_{n=1}^{\infty} f_n$. Applying the Monotone Convergence Theorem again yields
\begin{align*}
\int_{\Omega} \sum_{n=1}^{\infty} f_n\, d\mu &= \int_{\Omega} \lim_{N\to\infty} g_N \, d\mu \\ &=
\lim_{N\to \infty} \int_{\Omega} g_N \, d\mu \\ &= \lim_{N\to\infty} \sum_{n=1}^{N} \int_{\Omega} f_n\, d\mu\\ &=\sum_{n=1}^{\infty} \int_{\Omega} f_n\, d\mu.
\end{align*}
Proposition F.3.5.
Let $(\Omega,\mathcal{F},\mu)$ be a measure space. For any two non-negative measurable functions $f,g:\Omega\to [0,\infty]$,
- $\phi(E)=\int_E f\, d\mu$ is a measure function on $(\Omega,\mathcal{F})$, and
-
\[ \int_{\Omega} g\, d\phi = \int_{\Omega} gf \, d\mu.\]
We say in this case that $\phi$ has a density $f$ with respect to $\mu$, and write $d\phi=fd\mu$.
Proof.
It is easy to see that $\phi(E)\geq 0$ for all $E\in\mathcal{F}$ and $\phi(\emptyset)=0$. We next show that $\phi$ is countable additive. Let $E_n, n\in\mathbb{N}$ be a sequence of disjoint sets whose union equals $E$. Corollary F.3.1 implies that
\begin{align} \tag{*}
\phi(E) = \int_{\Omega} f I_E\,d\mu = \int_{\Omega} \sum_{n=1}^{\infty} f I_{E_n} \,d\mu = \sum_{n=1}^{\infty} \int f I_{E_n}\,d\mu = \sum_{n=1}^{\infty} \phi(E_n).
\end{align}
The second statement above follows from the first statement whenever $g$ is an indicator function $g(x)=cI_A(x)$. Similar arguments show that the second statement follows from the first statement whenever $g$ is a simple function. The case of a general function $g$ follows from approximating $g$ by a sequence of simple functions $0\leq s_1\leq s_2\leq\cdots$ (Proposition F.3.1) and using the Monotone Convergence Theorem twice
\[ \int_{\Omega} g \, d\phi = \int_{\Omega} \lim_n s_n \, d\phi = \lim_n \int_{\Omega} s_n\,d \phi = \lim_n \int_{\Omega} s_n f\,d\mu = \int_{\Omega} g f\,d\mu.\]
Proposition F.3.6 (Fatou's Lemma).
For any sequence of non-negative measurable functions $f_n, n\in\mathbb{N}$,
\[ \int_{\Omega} \liminf_{n\to\infty} f_n\,d\mu \leq \liminf_{n\to\infty} \int_{\Omega} f_n\,d\mu.\]
Proof.
Defining the function $g_k(x)=\inf\{f_i(x): i\geq k\}$, we have $g_k\leq f_k$ and therefore for all $k\in\mathbb{N}$,
\[\int_{\Omega} g_k\,d\mu\leq \int_{\Omega} f_k \,d\mu.\]
Since $0\leq g_1\leq g_2\leq\cdots$, and $g_k\to\liminf_n f_n$, we can apply the Monotone convergence theorem to the left hand side above to get
\[ \int_{\Omega} \liminf_n f_n\,d\mu =
\lim_k \int_{\Omega} g_k\,d\mu
=\liminf_k \int_{\Omega} g_k\,d\mu
\leq \liminf_k \int_{\Omega} f_k \,d\mu.\]
The definition of the Lebesgue integral $\int_A f\, d\mu$ thus far has been restricted to non-negative functions $f$. We generalize this below to real valued functions $f:\Omega\to\R$.
Definition F.3.4.
For a function $f:\Omega\to\R$ we define its positive and negative parts
\begin{align*}
f^+(\omega) &= \begin{cases} f(\omega) & f(\omega)\geq 0\\ 0 & f(\omega)<0\end{cases}\\
f^-(\omega) &= \begin{cases} -f(\omega) & f(\omega)\leq 0\\ 0 & f(\omega)>0\end{cases}.
\end{align*}
This implies the following decomposition of an arbitrary function $f:\Omega\to\R$ to its positive and negative parts:
\[ f(\omega) = f^+ + f^-.\]
Definition F.3.5.
The Lebesgue integral of a measurable function $f:\Omega \to \R$ is
\[ \int_{\Omega} f \, d\mu \defeq \int_{\Omega} f^+\,d\mu - \int_{\Omega} f^- \, d\mu\]
where $\int f^+\, d\mu$ and $\int f^-\,d\mu$ are integrals of non-negative functions defined in Definition F.3.3. If the integral above is finite we say that $f$ is $\mu$-integrable or simply integrable.
If both $\int f^+\, d\mu= \infty$ and $\int f^-\,d\mu = \infty$ in the definition above we say that the integral above does not exist.
Proposition F.3.7.
\[ \Big| \int_{\Omega} f\,d\mu \Big| \,\,\leq\,\, \int_{\Omega} |f|\,d\mu.\]
Proof.
The left hand side equals $\int f^+\,d\mu - \int f^-\,d\mu$, a difference of two non-negative quantities. This is clearly smaller than the right hand side, which equals $\int |f^+|\,d\mu + \int |f^-|\,d\mu$.
Proposition F.3.8.
Let $f,g$ be two measurable functions and $\alpha,\beta\in\R$. Then
\[\int_{\Omega} \alpha f+\beta g\,d\mu = \alpha\int_{\Omega} f\,d\mu + \beta\int_{\Omega} g\, d\mu.\]
Proof.
We decompose the proof into the case $\int_{\Omega} f+g\,d\mu = \int_{\Omega} f\,d\mu + \int_{\Omega} g\, d\mu$ and the case $\int_{\Omega} \alpha f \,d\mu = \alpha \int_{\Omega} f\,d\mu$. Both cases together imply the proposition above.
In the first case, if $\alpha > 0$ the result follows from applying Corollary F.3.1 to the positive-negative decomposition
\[\int \alpha f\, d\mu = \int (\alpha f)^+ \, d\mu - \int (\alpha f)^- \, d\mu = \alpha \int f^+ \, d\mu - \alpha \int f^- \, d\mu = \alpha \int f\,d\mu.\]
Similarly, if $\alpha<0$
\begin{align*}
\int \alpha f\, d\mu &= \int (\alpha f)^+ \, d\mu - \int (\alpha f)^- \, d\mu \\ &=
\int (-\alpha f^-) \, d\mu - \int (-\alpha f^+) \, d\mu \\
&= -\alpha \int f^- \, d\mu - (-\alpha) \int f^+ \, d\mu = \alpha \int f\,d\mu.
\end{align*}
In the second case, the result follows from applying Corollary F.3.1 to the positive-negative decomposition of $f+g$
\begin{align*}
\int f+g\,d\mu
&= \int f^+ - f^- + g^+ - g^-\,d\mu \\
&= \int f^+\,d\mu - \int f^-\,d\mu + \int g^+\,d\mu - \int g^- \, d\mu \\
&= \int f\,d\mu + \int g\,d\mu.
\end{align*}
Proposition F.3.9 (Dominated Convergence Theorem).
If $f_n\to f$ and $|f_n(x)| \leq g(x)$ for all $n\in\mathbb{N}$ for some integrable function $g$, then
\begin{align}
&\int_{\Omega} \Big|f_n-f\Big|\,d\mu \to 0\\
&\int_{\Omega} f_n\,d\mu \to \int_{\Omega} f \,d\mu.
\end{align}
Proof.
We denote $f=\lim f_n$ and observe that $f_n$ is integrable since $|f_n|\leq g$ and $g$ is integrable. Applying Fatou's lemma to the sequence of non-negative functions $2g-|f_n-f|\geq 0$ we get
\begin{align*}
\int 2g \,d\mu &\leq \liminf_{n\to\infty} \int (2g-|f_n-f|)\,d\mu =
\int 2g\,d\mu + \liminf_{n\to\infty} - \int |f_n-f|\,d\mu\\ & =
\int 2g\,d\mu - \limsup_{n\to\infty} \int |f_n-f|\,d\mu,
\end{align*}
which implies
\begin{align*}
0 \geq \limsup_{n\to\infty} \int |f_n-f|\,d\mu.
\end{align*}
Since $\int |f_n-f|\,d\mu$ is a sequence of non-negative values, the first result holds. The second result follows from applying Proposition F.3.7 to $f_n-f$:
\begin{align*}
0 &= \lim_{n\to\infty} \int_{n\to\infty} |f_n-f|\,d\mu \\
&\geq \lim_{n\to\infty} \Big|\int f_n-f \,d\mu\Big | \\
&= \lim_{n\to\infty} \Big| \int f_n\,d\mu - \int f \,d\mu \Big |.
\end{align*}
Corollary F.3.2 (Bounded Convergence Theorem).
If $\mu(\Omega) < \infty$, $f_n\to f$, and for some finite $M$, $|f_n(x)| < M$ for all $n$ and all $x$, then
\begin{align*}
\int_{\Omega} f_n\,d\mu \to \int_{\Omega} f \,d\mu.
\end{align*}
Proof.
The result follows immediately from the second statement of the dominated convergence theorem above.
Most of the propositions in this section are specified in terms of an integral of a function $f$ over the measurable space $\Omega$. These propositions remain true if the integrand $f$ is replaced by $fI_A$, effectively creating new versions of these propositions where the integrals range over alternative sets $A$ rather than $\Omega$. As an example, consider a modified version of Proposition F.3.8, which states that
\[\int_{A} \alpha f+\beta g\,d\mu = \alpha\int_{A} f\,d\mu + \beta\int_{A} g\, d\mu.\]
Definition F.3.6 Let $(\Omega,\mathcal{F},\mu)$ be a measure space. We say that a property holds almost everywhere, abbreviated a.e., if it holds on $\Omega\setminus{S}$ where $\mu(S)=0$. In other words, the property holds everywhere except on a set of measure zero.
Proposition F.3.10.
Let $f$ be a non-negative function. Then
\[ \int f\,d\mu =0 \qquad \text{implies} \qquad f=0 \text{ a.e.}.\]
Proof.
Defining $E_n$ to be the subset of $\Omega$ on which $f>1/n$, we have $f\geq \sum_{n\in\mathbb{N}} (1/n) I_{E_n}$ and
\[ 0=\int f\,d\mu \geq \int \sum_{n\in\mathbb{N}} (1/n) I_{E_n}\,d\mu =
\sum_{n\in\mathbb{N}} (1/n) \mu(E_n).\]
It follows that $\mu(E_n)=0$ for all $n\in\mathbb{N}$, implying that
$\mu(\cup_{n\in\mathbb{N}}E_n) \leq \sum_{n\in\mathbb{N}}\mu(E_n)=0$ and therefore $f=0$ except on a set of measure zero.
Corollary F.3.3.
If $\int(f-g)^2\,d\mu=0$ or $\int|f-g|\,d\mu=0$ then $f=g$ a.e..
F.3.1 Relation between the Riemann and the Lebesgue Integrals*
The following proposition states precisely when a function is Riemann integrable. It also states that if the Riemann integral exists then the Lebesgue integral exists as well and the two integrals agree in value.
Proposition F.3.11.
Let $f:[a,b]\to\R$ be a bounded function. Then it is Riemann integrable if and only if it is continuous a.e.. Furthermore, $f$ then is also integrable with respect to the Lebesgue measure, and the two integrals agree in value.
Proof.
We use notations below from the section concerning Riemann integrals. To distinguish between the Riemann and the Lebesgue integrals we denote the former as $\int f\,dx$ and the latter as $\int f\,d\mu$ ($\mu$ here corresponds to the Lebesgue measure). All integrals in the proof below are over the interval $[a,b]$.
We construct a sequence of partitions $P_n, n\in\mathbb{N}$ such that $P_k$ is a refinement of $P_{k-1}$, the distance between adjacent points in $P_k$ is less than $1/k$, and
\begin{align*}
\lim_{k\to\infty} U(P_k,f)&=\overline{\int f\,dx}\\
\lim_{k\to\infty} L(P_k,f)&=\underline{\int f\,dx}.
\end{align*}
(This is possible since the lower and upper Riemann integrals are defined using the limits above.) Defining the following two simple functions
\begin{align}
L(x) &= \begin{cases} m_i & x\in\Delta_i\\ f(a) & x=a \\ f(b) & x=b\end{cases}\\
U(x) &= \begin{cases} M_i & x\in\Delta_i\\ f(a) & x=a \\ f(b) & x=b\end{cases}.
\end{align}
we have
\begin{align*}
L(P_k,f)&=\int L_k\,d\mu \\
U(P_k,f)&=\int U_k\,d\mu \\
L_1\leq L_2\leq \cdots\leq &f\leq \cdots\leq U_2\leq U_l \quad \text{(since } P_k \text{ refines } P_{k-1}).
\end{align*}
The last equation above implies that $L_k$ and $U_k$ converge to limit functions $L(x)=\lim_{n\to\infty} L_k(x)$ and $U(x)=\lim_{n\to\infty} U_k(x)$ and that $L\leq f\leq U$. Using the Monotone Convergence Theorem, we have
\[ \int L\,d\mu = \underline{\int f\,dx},\qquad
\int U\,d\mu = \overline{\int f\,dx}.\]
Note that the above derivations assume only that $f$ is bounded. The function $f$ is Riemann integrable, if and only if the lower and upper integrals agree, which occurs if and only if $L=U$ a.e. (using the fact that $U-L\geq 0$ and Proposition F.3.10) or equivalently $L=f=U$. This proves that if $f$ is a bounded Riemann integrable function, it is also Lebesgue integrable with respect to the Lebesgue measure and the two integrals agree.
If $x$ is not equal to one of the points in the partition $P_k$, then $L(x)=U(x)$ if and only if $m_i=M_i$, which occurs if and only if $f$ is continuous at $x$. Recalling that $f$ is Riemann integrable if and only if $L=U$ a.e. (shown above), we have that $f$ is Riemann integrable if and only if $f$ is continuous a.e..
F.3.2 Transformed Measures*
Definition F.3.7.
Consider a measure space $(\Omega,\mathcal{F},\mu)$, and a measurable function $T:\Omega\to\Omega'$ where $(\Omega',\mathcal{F}')$ is a measurable space. The transformed measure $\mu T^{-1}$ is a measure on $(\Omega',\mathcal{F}')$ defined as follows
\[\mu T^{-1}(A) = \mu(T^{-1}A), \qquad A\in\mathcal{F}'.\]
It is straightforward to verify that $\mu T^{-1}$ satisfy the conditions of non-negativity and countable additivity, and is therefore a legitimate measure function. The following proposition uses this concept to construct the well-known change of variable formula for the Lebesgue integral.
Proposition F.3.12 (Change of Variable).
Let $f:\Omega'\to\R$ be a non-negative measurable function. Then
\begin{align} \tag{**}
\int_{T^{-1}(A')} f(Tx)\mu(dx) = \int_{A'} f(x')\mu T^{-1}(dx'), \qquad A\in\Omega'.
\end{align}
The change of variable formula above holds also for a real valued $f$ (not necessarily non-negative) if $f\circ T$ is integrable with respect to $\mu$.
Proof.
If $f=I_A$ then $f\circ T=I_{T^{-1}A}$ and (**) holds by definition of the Lebesgue integral and the transformed measure. The linearity of the integral implies that (**) holds also for non-negative simple function. The change of variable formula (**) holds for non-negative function by constructing a sequence of simple functions $s_n, n\in\mathbb{N}$ such that $s_n\nearrow f$ and using the Monotone Convergence Theorem.
If $f$ is a real valued function, we can apply (**) to $|f|$, which implies that $f$ is integrable with respect to $\mu T^{-1}$ if $f\circ T$ is integrable with respect to $\mu$. The result then follows by decomposing $f$ to its positive and negative parts and using the first part of the proposition on these two non-negative functions.
Proposition F.2.3 derives a special case of the change of variables formula that is often useful in computing non-trivial integrals.