Probability
The Analysis of Data, volume 1
Set Theory: Basic Definitions
$
\def\P{\mathsf{P}}
\def\R{\mathbb{R}}
\def\defeq{\stackrel{\tiny\text{def}}{=}}
\def\c{\,|\,}
$
A.1. Basic Definitions
This chapter describes set theory, a mathematical theory that underlies all of modern mathematics.
Definition A.1.1.
A set is an unordered collection of elements.
Sets may be described by listing their elements between curly braces, for example $\{1,2,3\}$ is the set containing the elements 1, 2, and 3. Alternatively, we an describe a set by specifying a certain condition whose elements satisfy, for example $\{x: x^2=1\}$ is the set containing the elements $1$ and $-1$ (assuming $x$ is a real number).
We make the following observations.
- There is no importance to the order in which the elements of a set appear. Thus $\{1,2,3\}$, is the same set as $\{3,2,1\}$.
- An element may either appear in a set or not, but it may not appear more than one time.
- Sets are typically denoted by an uppercase letter, for example $A$ or $B$.
- It is possible that the elements of a set are sets themselves, for example $\{1,2,\{3,4\}\}$ is a set containing three elements (two scalars and one set). We typically denote such sets with calligraphic
notation, for example $\mathcal{U}$.
Definition A.1.2.
If $a$ is an element in a set $A$, we write $a\in A$. If $a$ is not an element of $A$, we write $a\not\in A$. The empty set, denoted by $\emptyset$ or $\{\}$, does not contain any element.
Definition A.1.3.
A set $A$ with a finite number of elements is called a finite set and its size (number of elements) is denoted by $|A|$. A set with an infinite number of elements is called an infinite set.
Definition A.1.4.
We denote $A\subset B$ if all elements in $A$ are also in $B$. We
denote $A=B$ if $A\subset B$ and $B\subset A$, implying that the two
sets are identical. The difference between two sets $A\setminus B$ is
the set of elements in $A$ but not in $B$. The complement of a set $A$
with respect to a set $\Omega$ is $A^c=\Omega\setminus A$ (we may omit
the set $\Omega$ if it is obvious from context). The symmetric
difference between two sets $A,B$ is
\[ A\triangle B = \{x: x\in A\setminus B \text{ or } x\in B\setminus A\}.\]
Example A.1.1.
We have $\{1,2,3\}\setminus \{3,4\}=\{1,2\}$ and $\{1,2,3\}\triangle
\{3,4\}=\{1,2,4\}$. Assuming $\Omega=\{1,2,3,4,5\}$, we have
$\{1,2,3\}^c=\{4,5\}$.
In many cases we consider multiple sets indexed by a finite or
infinite set. For example $U_{\alpha}, \alpha\in A$ represents
multiple sets, one set for each element of $A$.
Example A.1.2.
Below are three examples of multiple sets, $U_{\alpha}, \alpha\in A$.
The first example shows two sets: $\{1\}$ and $\{2\}$. The second
example shows multiple sets: $\{1,-1\}$, $\{2,-2\}$, $\{3,-3\}$, and
so on. The third example shows multiple sets, each containing all real
numbers between two consecutive natural numbers.
\begin{align*}
U_i&=\{i\},& i&\in A=\{1,2\},\\
U_i&=\{i,-i\},& i&\in A=\mathbb{N}=\{1,2,3,\ldots\},\\
U_{\alpha}&=\{\alpha+r: 0\leq r \leq 1\}, & \alpha&\in
A=\mathbb{N}=\{1,2,3,\ldots\}.
\end{align*}
Definition A.1.5.
For multiple sets $U_{\alpha}, \alpha\in A$ we define the union and
intersection operations as follows:
\begin{align*}
\bigcup_{\alpha\in A} U_{\alpha} & =\{u: u\in U_{\alpha} \text{ for
one or more } \alpha\in A\}\\
\bigcap_{\alpha\in A} U_{\alpha} & =\{u: u\in U_{\alpha} \text{ for
all } \alpha\in A\}.
\end{align*}
Figure A.1.1 below illustrates these concepts in the case of
two sets $A,B$ with a non-empty intersection.
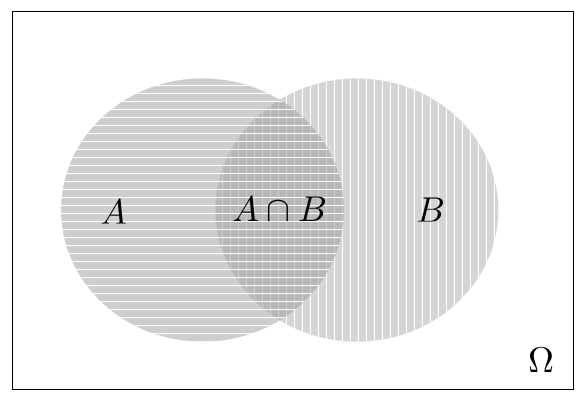
Figure 1.2.1: Two circular sets $A,B$, their intersection $A\cap B$ (gray area with horizontal and vertical lines), and their union $A\cup B$ (gray area with either horizontal or vertical lines or both). The set $\Omega\setminus (A\cup B)=(A\cup B)^c=A^c\cap B^c$ is represented by white color.
Definition A.1.6.
The sets $U_{\alpha}, \alpha\in A$ are mutually disjoint if
$\cap_{\alpha\in A}U_{\alpha}=\emptyset$ and are pairwise disjoint if
$\alpha\neq\beta$ implies $U_{\alpha}\cap U_{\beta}=\emptyset$. A
union of pairwise disjoint sets $U_{\alpha}$, $\alpha\in A$ is denoted
by $\uplus_{\alpha\in A} U_{\alpha}$.
Example A.1.3.
\begin{align*}
\{a,b,c\}\cap\{c,d,e\}&=\{c\}\\ \{a,b,c\}\cup\{c,d,e\}&=\{a,b,c,d,e\}\\
\{a,b,c\}\setminus\{c,d,e\}&=\{a,b\}.
\end{align*}
Example A.1.4.
If $A_1=\{1\}, A_2=\{1,2\}, A_3=\{1,2,3\}$ we have
\begin{align*}
\{A_i: i\in \{1,2,3\}\}&=\{\{1\},\{1,2\},\{1,2,3\}\}\\
\bigcup_{i\in\{1,2,3\}} A_i &= \{1,2,3\}\\
\bigcap_{i\in\{1,2,3\}} A_i &= \{1\}.
\end{align*}
The properties below are direct consequences of the definitions above.
Proposition A.1.1.
For all sets $A,B,C\subset \Omega$,
- Union and intersection are commutative and distributive:
\begin{align*} A\cup B=B\cup A, \quad (A\cup B)\cup C = A\cup (B\cup C)\\
A\cap B=B\cap A, \quad (A\cap B)\cap C = A\cap (B\cap C)
\end{align*}
- $(A^c)^c=A, \quad \emptyset^c=\Omega,\quad \Omega^c=\emptyset$
- $\emptyset\subset A$
- $A\subset A$
- $A\subset B$ and $B\subset C$ implies $A\subset C$
- $A\subset B$ if and only if $B^c\subset A^c$
- $A\cup A=A=A\cap A$
- $A\cup\Omega = \Omega, \quad A\cap\Omega = A$
- $A\cup\emptyset = A, \quad A\cap\emptyset = \emptyset$.
Definition A.1.7.
The power set of a set $A$ is the set of all subsets of $A$, including
the empty set $\emptyset$ and $A$. It is denoted by $2^A$.
Proposition A.1.2.
If $A$ is a finite set then
\[ |2^A| = 2^{|A|}.\]
Proof.
We can describe each element of $2^A$ by a list of $|A|$ 0 or 1 digits
(1 if the corresponding element is selected and 0 otherwise). The
proposition follows since there are $2^{|A|}$ such lists (see
Proposition 1.6.1).
Example A.1.5.
\begin{align*}
2^{\{a,b\}} &= \{\emptyset,\{a,b\},\{a\},\{b\}\}\\
|2^{\{a,b\}}|&=4\\
\sum_{A\in2^{\{a,b\}}} |A| &= 0+2+1+1= 4.
\end{align*}
The R package sets is convenient for illustrating basic concepts. For example, the code below examines the power set of three different finite sets.
library(sets)
A = set("a", "b", "c")
2^A
## {{}, {"a"}, {"b"}, {"c"}, {"a", "b"}, {"a",
## "c"}, {"b", "c"}, {"a", "b", "c"}}
A = set("a", "b", set("a", "b"))
2^A
## {{}, {"a"}, {"b"}, {{"a", "b"}}, {"a", "b"},
## {"a", {"a", "b"}}, {"b", {"a", "b"}}, {"a",
## "b", {"a", "b"}}}
A = set(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
length(2^A)
Proposition A.1.3. (Distributive Law of Sets)
\begin{align*}
\left(\bigcup_{\alpha\in Q} A_{\alpha}\right) \bigcap C &=
\bigcup_{\alpha\in Q} \left(A_{\alpha} \bigcap C\right)\\
\left(\bigcap_{\alpha\in Q} A_{\alpha}\right) \bigcup C &=
\bigcap_{\alpha\in Q} \left(A_{\alpha} \bigcup C\right).
\end{align*}
Proof.
We prove the first statement for the case of $|Q|=2$. The proof of the
second statement is similar, and the general case is a straightforward
extension.
We prove the set equality $U=V$ by showing $U\subset V$ and $V\subset
U$. Let $x$ belong to the set $(A\cup B)\cap C$. This means that $x$
is in $C$ and also in either $A$ or $B$, which implies $x\in (A\cap
C)\cup(B\cap C)$. On the other hand, if $x$ belongs to $(A\cap
C)\cup(B\cap C)$, $x$ is in $A\cap C$ or in $B\cap C$. Therefore $x\in
C$ and also $x$ is in either $A$ or $B$, implying that $x\in (A\cup
B)\cap C$.
Proposition A.1.4.
\begin{align*}
S\setminus \bigcup_{\alpha\in Q} A_{\alpha} &= \bigcap_{\alpha\in Q}
(S\setminus A_{\alpha})\\
S\setminus \bigcap_{\alpha\in Q} A_{\alpha} &= \bigcup_{\alpha\in Q}
(S\setminus A_{\alpha}).
\end{align*}
Proof.
We prove the first result. The proof of the second result is similar. Let $x\in S\setminus \cup_{\alpha\in Q} A_{\alpha}$. This implies that $x$ is in $S$ but not in any of the $A_{\alpha}$ sets, which implies
$x\in S\setminus A_{\alpha}$ for all $\alpha$, and therefore $x\in \cap_{\alpha\in Q} (S\setminus A_{\alpha})$. On the other hand, if $x\in \cap_{\alpha\in Q} (S\setminus A_{\alpha})$, then $x$ is in each
of the $S\setminus A_{\alpha}$ sets. Therefore $x$ is in $S$ but not in any of the $A_{\alpha}$ sets, hence $x\in S\setminus \cup_{\alpha\in Q} A_{\alpha}$.
Corollary A.1.1 (De-Morgan's Law).
\begin{align*}
\left(\bigcup_{\alpha\in Q} A_{\alpha}\right)^c &= \bigcap_{\alpha\in
Q} A_{\alpha}^c\\
\left(\bigcap_{\alpha\in Q} A_{\alpha}\right)^c &= \bigcup_{\alpha\in
Q} A_{\alpha}^c.
\end{align*}
Proof.
This is a direct corollary of the previous proposition with $S=\Omega$.
Definition A.1.8.
We define the sets of all natural numbers, integers, and rational
numbers as follows:
\begin{align*}
\mathbb{N} &= \{1,2,3,\ldots\}\\
\mathbb{Z} &= \{\ldots,-1,0,1,\ldots\}\\
\mathbb{Q} &= \{p/q:p\in\mathbb{Z},q\in\mathbb{Z}\setminus\{0\}\}.
\end{align*}
The set of real numbers is denoted by $\R$.
One way to rigorously define the set
of real numbers is as the completion of the rational numbers. The
details may be found in standard real analysis textbooks, for example
(Rudin, 1976). We do not pursue this formal definition here.
Definition A.1.9.
We denote the closed interval, the open interval and the two types of
half-open intervals between $a,b\in\R$ as
\begin{align*}
[a,b] &= \{x\in\R : a \leq x \leq b \}\\
(a,b) &= \{x\in\R : a < x < b \}\\
\end{align*}
\begin{align*}
[a,b) &= \{x\in\R : a \leq x < b \}\\
(a,b] &= \{x\in\R : a < x \leq b \}.
\end{align*}
Example A.1.6.
\begin{align*}
\bigcup_{n\in\mathbb{N}}[0,n/(n+1))&=[0,1),\\
\bigcap_{n\in\mathbb{N}} [0,n/(n+1))&=[0,1/2).
\end{align*}
Definition A.1.10.
The Cartesian product of two sets $A$ and $B$ is
\[A\times B=\{(a,b):a\in A,b\in B\}.\]
In a similar way we define the Cartesian product of $n\in\mathbb{N}$
sets. The repeated Cartesian product of the same set, denoted as
\[A^d= A\times \cdots\times A, \qquad d\in\mathbb{N},\]
is the set of $d$-tuples or $d$-dimensional vectors whose components
are elements in $A$.
Example A.1.7.
$\R^d$ is the set of all $d$ dimensional vectors whose
components are real numbers.
Definition A.1.11.
A relation $R$ on a set $A$ is a subset of $A\times A$, or in other
words a set of pairs of elements in $A$. If $(a,b)\in R$ we denote
$a\sim b$ and if $(a,b)\not\in R$ we denote $a\not\sim b$. A relation
is reflexive if $a\sim a$ for all $a\in A$. It is symmetric if $a\sim
b$ implies $b\sim a$ for all $a,b\in A$. It is transitive if $a\sim b$
and $b\sim c$ implies $a\sim c$ for all $a,b,c\in A$. An equivalence
relation is a relation that is reflexive, symmetric, and transitive.
Example A.1.8.
Consider relation 1 where $a\sim b$ if $a\leq b$ over
$\mathbb{R}$ and relation 2 where $a\sim b$ if $a=b$ over
$\mathbb{Z}$. Relation 1 is reflexive and transitive but not
symmetric. Relation 2 is reflexive, symmetric, and transitive and is
therefore an equivalence relation.
Definition A.1.12.
The sets $U_{\alpha}, \alpha\in A$ form a partition of $U$ if
\[ \biguplus_{\alpha\in A} U_{\alpha} = U.\]
In other words, the union of the pairwise disjoint sets $U_{\alpha}, \alpha\in A$ is $U$. The sets $U_{\alpha}$ are called equivalence classes.
An equivalence relation $\sim$ on $A$ induces a partition of $A$ as
follows: $a\sim b$ if and only if $a$ and $b$ are in the same
equivalence class.
Example A.1.9.
Consider the set $A$ of all cities and the relation $a\sim b$ if the
cities $a,b$ are in the same country. This relation is reflexive,
symmetric, and transitive, and therefore is an equivalence relation.
This equivalence relation induces a partition of all cities into
equivalence classes consisting of all cities in the same country. The
number of equivalence classes is the number of countries.
