Probability

The Analysis of Data, volume 1

Random Processes: The Borel-Cantelli Lemmas and the Zero-One Law*

6.6. The Borel-Cantelli Lemmas and the Zero-One Law*

This section contains advanced material concerning probabilities of infinite sequence of events. The results rely on limits of sets, introduced in Section A.4. In particular, we use the concept of $\limsup A_n$ for a sequence of sets $A_n, n\in\mathbb{N}$ and its interpretation as $A_n$ infinitely often (abbreviated i.o.).

Proposition 6.6.1 (The First Borel-Cantelli Lemma). For any sequence of events $A_n$, $n\in\mathbb{N}$ \[\sum_{n\in\mathbb{N}}\P(A_n) < \infty \qquad \text{implies}\qquad \P(A_n \text{ i.o.})=0.\]
Proof. Note that $\limsup_n A_n\subset \cup_{k=m}^{\infty} A_k$ (see Section A.4), implying that \[ \P(\limsup A_n) \leq \P(\cup_{k\geq m} A_k) \leq \sum_{k\geq m} \P(A_k).\] Since $\sum_{n\in\mathbb{N}}\P(A_n) < \infty$, it follows that the right hand side above converges to 0 as $m\to\infty$. Since the inequality above holds for all $m$, $\P(\limsup A_n)=0$.
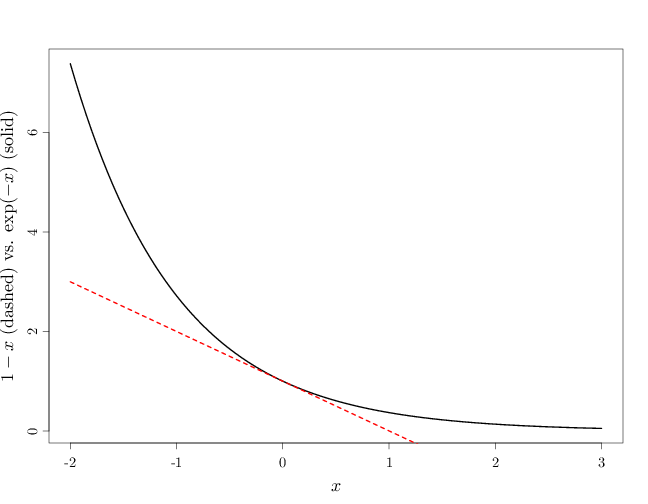
Lemma 6.6.1. \[ 1-x\leq \exp(-x), \qquad \forall x\in\R.\]
Proof. The first derivative of $1-x$ is $-1$ and the second is 0. The first derivative of $\exp(-x)$ is $-\exp(-x)$ and the second is $\exp(-x)$. Both the two functions and their first derivatives agree at 0. Since $(\exp(-x))''\geq (1-x)''$ for all $x$, it follows that $(\exp(-x))'$ will be larger than $(1-x)'$ for positive $x$ and smaller for negative $x$. It follows that $\exp(-x)$ will decay more slowly as $x>0$ increases and grow faster as $x<0$ decreases. This establishes the desired inequality.

The R code below graphs the two functions $1-x$ (dashed) and $\exp(-x)$.

par(cex.main = 1.5, cex.axis = 1.2, cex.lab = 1.5)
curve(exp(-x), ylab = "$1-x$ (dashed) vs. $\\exp(-x)$ (solid)",
    lwd = 3, from = -2, to = 3, xlab = "$x$")
curve(1 - x, add = TRUE, col = "red", lty = 2, lwd = 3)
Proposition 6.6.2 (The Second Borel-Cantelli Lemma). For a sequence of independent events $A_n, n\in\mathbb{N}$, \[\sum_{n\in\mathbb{N}}\P(A_n)=+\infty \qquad \text{implies} \qquad \P(A_n \text{ i.o.})=1.\]
Proof. Since the events $A_n, n\in\mathbb{N}$ are independent, their complements $A_n^c, n\in\mathbb{N}$ are independent as well (see Proposition E.4.1). Using the bound in Lemma 6.6.1, we have \begin{align} \P\left(\bigcap_{k=n}^{n+r} A_n^c\right)=\prod_{k=n}^{n+r} (1-\P(A_k))\leq \exp\left(-\sum_{k=n}^{n+r} \P(A_k)\right). \end{align} Since $\sum_{n\in\mathbb{N}} \P(A_n)=+\infty$, the right hand side above tends 0 as $r\to\infty$. It follows that \begin{align*} \P\left(\bigcap_{k=n}^{\infty} A_n^c\right)&=0\\ 1-\P(\limsup A_n) &= \P((\limsup A_n)^c) = \P\left(\bigcup_{n\in\mathbb{N}} \bigcap_{k\geq n} A_k^c\right) \leq \P\left(\bigcap_{k\geq n} A_k^c\right)=0. \end{align*}
Definition 6.6.1. Let $A_n,n\in\mathbb{N}$ be a sequence of events. The tail $\sigma$-algebra is \[ \mathcal{T}(\{A_n:n\in\mathbb{N}\}) \defeq \bigcap_{n\in\mathbb{N}} \sigma(\{A_m: m\geq n\}).\]

Intuitively, the tail $\sigma$-algebra contains events relating to the behavior of the tail of the sequence $A_n,n\in\mathbb{N}$.

Example 6.6.1 The events $A_k$, $A_k^c$ or $A_k\cap A_l$ are not members of the tail $\sigma$-algebra since there exists $\sigma(\{A_r, A_{r+1},\ldots\})$ that does not contain these events.

The event $\limsup A_n=\cap_{n\in\mathbb{N}} \cup_{k\geq n} A_k$ is an intersection of unions of tail events and therefore $\limsup A_n\subset \cup_{k\geq r} A_k$ for all $r$. As a result, $\limsup A_n\in \sigma(\{A_r, A_{r+1},\ldots\})$ for all $r$, implying that $\limsup A_n$ is a member of the tail $\sigma$-algebra. This is in agreement with the interpretation of $\limsup A_n$ as $A_n$ infinitely often, which depends only on the tail behavior and not on any particular $A_k$.

Proposition 6.6.3 (Kolmogorov's Zero-One Law) Let $A_n,n\in\mathbb{N}$ be independent events and $A\in\mathcal{T}(\{A_n: n\in\mathbb{N}\})$. Then $\P(A)=0$ or $\P(A)=1$.
Proof. By Corollary E.4.1, $\sigma(A_1),\ldots,\sigma(A_{n-1})$, $\sigma(\{A_n,A_{n+1},\ldots\})$ are independent, and since $A\in \sigma(\{A_n,A_{n+1},\ldots\})$, the sets $A,A_1,\ldots,A_{n-1}$ are independent. This holds for all $n$, implying that $A,A_1,A_2,\ldots$ are independent. Applying Corollary E.4.1 again, we have that $\sigma(A), \sigma(\{A_n: n\in\mathbb{N})$ are independent. Since $A\in \sigma(A)$ and $A\in \sigma(\{A_n: n\in\mathbb{N}\})$, $A$ is independent of itself, leading to $\P(A\cap A)=\P(A)\P(A)=(\P(A))^2$, and implying that $\P(A)=0$ or $\P(A)=1$.