Probability

The Analysis of Data, volume 1

Integration: The Riemann Integral

F.1. The Riemann Integral

Integration plays an important role in probability theory. We start by describing the Riemann integral, which is commonly taught in elementary calculus, and then describe the relationship between integration and differentiation. The next section covers the Lebesgue integral, which is technically harder than the Riemann integral and requires measure theory. The Lebesgue integral is needed for developing tools that are used to prove convergence results (Chapter 8). We conclude with several sections that extend integration and differentiation to multivariate functions.

Definition F.1.1. A partition of an interval $[a,b]$ is a finite set of points $Q=\{x_i: i=0,\ldots,n\}$ satisfying $a=x_0\leq x_1\leq \cdots \leq x_n=b$.
Definition F.1.2. Given a bounded function $f:[a,b]\to\R$ and a partition of $[a,b]$ we define \begin{align*} M_i&=\sup_{x\in \Delta_i} f(x) \\ m_i&=\inf_{x\in\Delta_i} f(x)\\ U(P,f)&=\sum_{i=1}^n M_i|\Delta_i|\\ L(P,f)&=\sum_{i=1}^n m_i|\Delta_i|. \end{align*} where $\Delta_i=(x_{i-1},x_i)$ and $|\Delta_i|=|x_{i-1}-x_i|$.

Figure F.1.1 shows a partition of four points and the corresponding $m_i$ and $M_i$ values. As the number of points in the partition increases the difference $|m_i-M_i|$ tend to decrease.

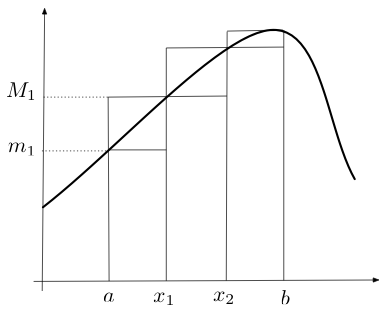
Partition of an interval

Figure F.1.1: A partition $\{a=x_0,x_1,x_2,b=a_3\}$ of $[a,b]$ and the corresponding $m_1$ and $M_1$ values.

Example F.1.1. Consider the function $f(x)=x$ over $[0,3]$ and the partition $Q=\{0,1,2,3\}$. Then $|\Delta_i|=1$, for all $i$, and $L(Q,f)=1\cdot 0+1\cdot 1+1\cdot 2$ and $U(Q,f)=1\cdot 1+1\cdot 2+2\cdot 3$. Clearly $M_i\geq m_i$, implying that $U(P,f)\geq L(P,f)$. As we add additional points to the partition the difference $U(P,f)- L(P,f)$ decays to zero.
Definition F.1.2. Let $f:[a,b]\to\R$ be a bounded function. Then \begin{align*} \overline{\int_a^b} f(x)\,dx &\defeq \inf_Q \,U(Q,f)\\ \underline{\int_a^b} f(x)\,dx &\defeq \sup_Q\, L(Q,f), \end{align*} where $\inf_Q$ and $\sup_Q$ above are taken over all possible partitions $Q$ of $[a,b]$. If the two quantities above are finite and equal, we say that $f$ is Riemann integrable over $[a,b]$ and denote the common value as \[ \int_a^b f(x)\,dx\defeq\overline{\int_a^b} f(x)\,dx=\overline{\int_a^b} f(x)\,dx.\]

We sometimes consider integrals over the entire real line, achieved by letting $a\to\infty$, $b\to-\infty$ in the definition above.

Definition F.1.3. A partition $Q$ is a refinement of a partition $P$ if every point in $P$ is also in $Q$. Given two partitions $P_1, P_2$, we define their common refinement as the partition composed of all the points that are either in $P_1$ or in $P_2$.
Proposition F.1.1. If $P'$ is a refinement of the partition $P$ then \begin{align*} L(P,f) &\leq L(P',f)\\ U(P',f) &\leq U(P,f). \end{align*}
Proof. We prove the first result. The proof of the second result is similar. We assume at first that $P'$ contains only one more point $x'$ ($x_i < x' < x_{i+1}$) than $P$. In this case $L(P',f)-L(P,f) = (m_i'\Delta_i'+ m_{i+1}'\Delta_{i+1}') - (m_i\Delta_i)$, and since $m_i',m_{i+1}'\geq m$ we have $L(P',f)-L(P,f)\geq 0$. If $P'$ contains several points in addition to $P$, we can repeat this argument several times to establish $L(P',f)-L(P,f)\geq 0$.
Proposition F.1.2. \[\overline{\int_a^b} f(x)\,dx \geq \underline{\int_a^b} f(x)\,dx.\]
Proof. Consider $Q$, a common refinement of two partitions $P_1$, $P_2$ of $[a,b]$. From Proposition F.1.1, it follows that \begin{align*} L(P_1,f) &\leq L(Q,f)\leq U(Q,f) \leq U(P_2,f). \end{align*} The above inequality holds for all $P_1$ and $P_2$. Taking supremum over all $P_1$ and infimum over all $P_2$ yields the desired result.
Proposition F.1.3. A bounded function $f:[a,b]\to R$ is Riemann integrable if and only if \[ \forall \epsilon>0,\,\exists Q \quad\text{such that} \quad U(Q,f)-L(Q,f) < \epsilon.\]
Proof. If $f$ is Riemann integrable, then for all $\epsilon>0$ there exists $P_1,P_2$ such that $U(P_2,f)-\int f\,dx < \epsilon/2$ and $\int f\,dx-L(P_1,f) < \epsilon/2$. If $Q$ is the common refinement of $P_1,P_2$, then using Proposition F.1.2, \[ U(Q,f) \leq U(P_2,f) < \int f\,dx + \epsilon/2 < L(P_1,f)+\epsilon \leq L(Q,f)+\epsilon.\] Conversely, we assume that for all $\epsilon>0$ there exists $Q$, such that $U(Q,f)-L(Q,f) < \epsilon$. For all partitions $P$ we have \[L(P,f)\leq \underline{\int_a^b f\,dx} \leq \overline{\int_a^b f\,dx}\leq U(P,f).\] and therefore for all $\epsilon>0$ \[0\leq \overline{\int_a^b f\,dx}-\underline{\int_a^b f\,dx} < \epsilon.\] Since $\epsilon$ is arbitrary, the function $f$ is Riemann integrable.
Corollary F.1.1. If $f:[a,b]\to\R$ is continuous, then it is Riemann integrable.
Proof. Since $[a,b]$ is compact, Proposition B.3.5 implies that $f$ is uniformly continuous on $[a,b]$. This implies that for all $\epsilon'<0$ these exists $\delta>0$ such that $|x-y| < \delta$ implies $|f(x)-f(y)| < \epsilon'$. If $P$ is a partition of $[a,b]$ such that $\delta_i < \delta$ for all $i$, then $M_i-m_i\leq \epsilon'$ and \[U(P,f)-L(P,f)=\sum_{i=1}^n (M_i-m_i)\Delta_i \leq \epsilon' \sum_{i=1}^n\Delta_i=\epsilon' (b-a).\] For all $\epsilon>0$ we can set $\epsilon'=\epsilon/(b-a)$, implying that $U(P,f)-L(P,f) < \epsilon$, and by Proposition F.1.3, $f$ is Riemann integrable.
Some standard properties of integrals are listed below.
Proposition F.1.4. The following properties apply to the Riemnan integral.
  1. Linearity: \[ \int_a^b af(x)+bg(x) \,dx = a\int_a^b f(x) \,dx+b\int_a^b g(x) \,dx.\]
  2. Interval Decomposition: for all $a\in (a,b)$ we have \[\int_a^b f(x) \,dx = \int_a^q f(x) \,dx +\int_q^b f(x) \,dx.\]
  3. \[\Big| \int_a^b f(x) \,dx \Big| \leq \int_a^b |f(x)| \,dx \leq \sup_{x\in[a,b]} |f(x)|\cdot |b-a|.\]
  4. If $f(x)\leq g(x)$ for all $x\in[a,b]$ then \[\int_a^b f\,dx \leq \int_a^b g\,dx.\]
Proof*. These properties follow from the corresponding properties of the Lebesgue integral (see Section F.3), and Proposition F.3.11, which implies that if $f$ is Riemann integrable, then it is Lebesgue integrable with respect to the Lebesgue measure, and the two integrals agree in value.
Proposition F.1.5. A function $f:[a,b]\to \R$ that is bounded and continuous except for a finite number of points at which it is perhaps discontinuous is Riemann integrable.
Proof*. Let $f$ be a bounded function that is continuous on $[a,b]$ except on $k$ points. By the second property above (interval decomposition), we can decompose the integral to $k+1$ integrals over continuous functions. Since each one of the integrals exists (see Corollary F.1.1), the integral of $f$ exists as well.

The above proposition shows that functions that are continuous and bounded except at a finite number of points are Riemann integrable. It does not specify which functions are not Riemann integrable. Proposition F.3.5 strengthen this claim and shows that a bounded function $f$ is Riemann integrable if and only if it is continuous almost everywhere (the phrase almost everywhere is made precise in Section F.3).