Relationships Between the Modes of Convergences

Probability

The Analysis of Data, volume 1

0
- Front Matter
- 0.1: Contents
- 0.2: Preface
1
2
- Random Variables
- 2.1: Basic Definitions
- 2.2: Functions of RVs
- 2.3: Expectation and Variance
- 2.4: Moments and MGF
- 2.5: RVs and Measure Theory
- 2.6: Notes
- 2.7: Exercises
3
4
5
- Important Vectors
- 5.1: Multinomial Vectors
- 5.2: Gaussian Vectors
- 5.3: Dirichlet Vectors
- 5.4: Mixture Vectors
- 5.5: Exponential Family
- 5.6: Notes
- 5.7: Exercises
6
- Random Processes
- 6.1: Basic Definitions
- 6.2: Marginals
- 6.3: Moments
- 6.4: Random Walk
- 6.5: Processes and Measure
- 6.6: Borell-Cantelli and Zero-One
- 6.7: Notes
- 6.8: Exercises
7
- Important RPs
- 7.1: Markov Chains
- 7.2: Poisson Process
- 7.3: Gaussian Process
- 7.4: Notes
- 7.5: Exercises
8
A
- Set Theory
- A.1: Basic Definition
- A.2: Functions
- A.3: Cardinality
- A.4: Limits of Sets
- A.5: Notes
- A.6: Exercises
B
- Metric Spaces
- B.1: Basic Definitions
- B.2: Limits
- B.3: Continuity
- B.4: Euclidean Space
- B.5: Growth of Functions
- B.6: Notes
- B.7: Exercises
C
- Linear Algebra
- C.1: Basic Definitions
- C.2: Rank
- C.3: Eigenvalues and Determinant
- C.4: Semidefinite Matrices
- C.5: SVD
- C.6: Notes
- C.7: Exercises
D
- Differentiation
- D.1: Scalar Differentiation
- D.2: Power and Taylor Series
- D.3: Notes
- D.4: Exercises
E
- Measure Theory
- E.1: Sigma Algebras
- E.2: Measure Function
- E.3: Extension Theorem
- E.4: Independence
- E.5: Important Measures
- E.6: Measurable Functions
- E.7: Notes
F

$\def\P{\mathsf{\sf P}} \def\E{\mathsf{\sf E}} \def\Var{\mathsf{\sf Var}} \def\Cov{\mathsf{\sf Cov}} \def\std{\mathsf{\sf std}} \def\Cor{\mathsf{\sf Cor}} \def\R{\mathbb{R}} \def\c{\,|\,} \def\bb{\boldsymbol} \def\diag{\mathsf{\sf diag}} \def\defeq{\stackrel{\tiny\text{def}}{=}} \newcommand{\toop}{\xrightarrow{\scriptsize{\text{p}}}} \newcommand{\tooas}{\xrightarrow{\scriptsize{\text{as}}}} \newcommand{\tooas}{\xrightarrow{\scriptsize{\text{as}}}} \newcommand{\tooas}{\xrightarrow{\scriptsize{\text{as}}}} \newcommand{\tooas}{\xrightarrow{\scriptsize{\text{as}}}} \newcommand{\tooas}{\xrightarrow{\scriptsize{\text{as}}}} \newcommand{\tood}{\rightsquigarrow} \newcommand{\iid}{\mbox{$\;\stackrel{\mbox{\tiny iid}}{\sim}\;$}}$

8.2. Relationships Between the Modes of Convergences

Proposition 8.2.1.

${\bb X}^{(n)} \tooas \bb X \quad \text{if and only if} \quad \P(\|{\bb X}^{(n)}-\bb X\| \geq \epsilon \text{ i.o.})=0, \quad \forall \epsilon>0.$

Proof. The event

$({\bb X}^{(n)}\tooas \bb X)^c$ is equivalent to the event

$\cup_{\epsilon>0} \{\|{\bb X}^{(n)}-\bb X\|\geq \epsilon \text{ i.o.}\}$ . It follows that the event

${\bb X}^{(n)}\tooas \bb X$ is equivalent to

$\P(\|{\bb X}^{(n)}-\bb X\|\geq \epsilon \text{ i.o.})=0$ for all

$\epsilon>0$ .

See Section A.4 for the definition of i.o. or infinitely often.

Proposition 8.2.2.

$\begin{align*} {\bb X}^{(n)} &\tooas \bb X \quad \text{implies} \quad {\bb X}^{(n)}\toop \bb X \\ {\bb X}^{(n)} &\toop \bb X \quad \text{implies} \quad {\bb X}^{(n)}\tood \bb X. \end{align*}$

Proof. We first show that convergence with probability 1 implies convergence in probability. Since

$\{\|{\bb X}^{(n)}-\bb X\|\geq \epsilon \text{ i.o.}\} =\limsup_n \{\|{\bb X}^{(n)}-\bb X\|\geq \epsilon\},$ the event

${\bb X}^{(n)}\tooas \bb X$ implies

$\begin{align*} \lim_n \P(\|{\bb X}^{(n)}-\bb X\|\geq \epsilon) &\leq \limsup_n \P(\|{\bb X}^{(n)}-\bb X\|\geq \epsilon) \\ &\leq \P\left(\limsup_n \|{\bb X}^{(n)}-\bb X\|\geq \epsilon\right) = 0. \end{align*}$ The inequality

$\limsup \P(A_n)\leq \P(\limsup A_n)$ follows from Fatou's lemma (see Chapter F) applied to the sequence of indicator functions

$f_n=I_{A_n}$ and the measure

$\mu=P$ . The last equality follows from the previous proposition.

We next show that convergence in probability implies convergence in distribution. Denoting $\bb 1=(1,\ldots,1)$ , we have that if ${\bb X}^{(n)}\leq {\bb x}$ then either ${\bb X}\leq \bb x+\epsilon \bb 1$ , or $\|\bb X - {\bb X}^{(n)} \| >\epsilon$ , or both (we interpret inequality between two vectors as a sequence of inequalities for the corresponding components: $\bb u\leq \bb v$ implies $u_i\leq v_i$ , $i=1,\ldots,d$ ). Similarly, if $\bb X\leq \bb x-\epsilon\bb 1$ then either ${\bb X}^{(n)}\leq \bb x$ or $\|\bb X - {\bb X}^{(n)} \| >\epsilon$ , or both. This implies that for all $n$ , $\begin{align*} F_{\bb X}^{(n)}(\bb x) &\leq \P({\bb X}\leq \bb x+\epsilon \bb 1) + \P(\|\bb X - {\bb X}^{(n)} \| >\epsilon) = F_{\bb X}(\bb x+\epsilon \bb 1) + \P(\|\bb X - {\bb X}^{(n)} \| >\epsilon) \\ F_{\bb X}(\bb x-\epsilon \bb 1) &\leq \P({\bb X}^{(n)}\leq \bb x) + \P(\|\bb X - {\bb X}^{(n)} \| >\epsilon) = F_{{\bb X}^{(n)}}(\bb x) + \P(\|\bb X - {\bb X}^{(n)} \| >\epsilon). \end{align*}$ Since ${\bb X}^{(n)}\toop \bb X$ , we have $\P(\|\bb X - {\bb X}^{(n)} \| >\epsilon)\to 0$ and letting $n\to\infty$ in the two inequalities above, we get $F_{\bb X}(\bb x-\epsilon \bb 1) \leq \liminf F_{{\bb X}^{(n)}}(\bb x)\leq \limsup F_{{\bb X}^{(n)}}(\bb x) \leq F_{\bb X}(\bb x+\epsilon \bb 1).$ The left hand side and the right hand side converge to $F_{\bb X}(\bb x)$ as $\epsilon\to 0$ at points $\bb x$ where $F_{\bb X}$ is continuous, implying that $F_{{\bb X}^{(n)}}(\bb x) \to F_{\bb X}(\bb x)$ .

The following example shows that convergence in probability may occur even if convergence with probability one does not occur.

Example 8.2.1. Consider

$\Omega=[0,1]$ with

$\P$ being the uniform distribution over

$\Omega$ . The sequence of random variables

$X^{(1)}=I_{(0,1/2]}$ ,

$X^{(2)}=I_{(1/2,1]}$ ,

$X^{(3)}=I_{(0,1/4]}$ ,

$X^{(5)}=I_{(1/4,1/2]}$ ,

$X^{(6)}=I_{(1/2,3/4]}$ , and so on, does not converge with probability one to any limit (for all

$\omega$ ,

$X^{(n)}(\omega)$ is a divergent sequence). On the other hand,

$X^{(n)}\toop 0$ since

$\P(|X^{(n)}|\geq \epsilon)\to 0$ for all

$\epsilon>0$ .

Proposition 8.2.3. If

$\bb c\in\R^d$ then

${\bb X}^{(n)}\tood \bb c \quad \text{if and only if} \quad {\bb X}^{(n)}\toop \bb c.$

Proof. It suffices to prove that convergence in distribution to a constant vector implies probability in probability (convergence in probability always implies convergence in distribution). We prove the result below for two dimensions

$d=2$ . The cases of other dimensions are similar.

We have (see Figure 8.2.1 below for an illustration) $\begin{align*} \P(\|{\bb X}^{(n)} -\bb c\|\leq\sqrt{2} \epsilon ) &= \P(\|{\bb X}^{(n)} -\bb c\|^2\leq 2 \epsilon^2 ) \\ &\geq \P(\bb c - \epsilon (1,1) < {\bb X}^{(n)} \leq \bb c+\epsilon(1,1)) \\ &= \P({\bb X}^{(n)}\leq \bb c+\epsilon(1,1)) - \P({\bb X}^{(n)}\leq \bb c+\epsilon(1,-1))\\ &\quad - \P({\bb X}^{(n)}\leq \bb c+\epsilon(-1,1))+ \P({\bb X}^{(n)}\leq \bb c+\epsilon(1,1)). \end{align*}$ In the first inequality above, we used the fact that if $|a_1-b_1|\leq \epsilon$ and $|a_2-b_2|\leq \epsilon$ then $\|\bb a-\bb b\|^2\leq 2\epsilon^2$ . In the second equality we used the principle of inclusion-exclusion (see Figure 8.2.1 for an illustration). If we have convergence in distribution ${\bb X}^{(n)}\tood \bb c$ , then the last term in the inequality above converges to $0+0+0+1$ , which implies convergence in probability ${\bb X}^{(n)}\toop \bb c$ .

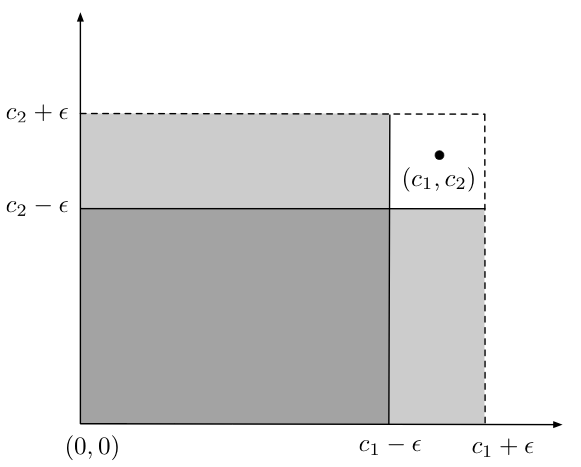
Figure illustrating proof

Figure 8.2.1: This figure illustrates the proof of Proposition 8.2.3. The white square region may be expressed as the region contained within the dashed rectangle minus the two shaded rectangles plus the intersection of the two shaded rectangles (since it was subtracted twice).

Proposition 8.2.4. The convergence

${\bb X}^{(n)}\toop \bb X$ occurs if and only if every sequence of natural numbers

$n_1,n_2,\ldots\in \mathbb{N}$ has a subsequence

$r_1, r_2,\ldots\in\{n_1,n_2,\ldots\}$ such that

${\bb X}^{(r_k)}\tooas \bb X$ as

$k\to\infty$ .

Proof. We assume that

${\bb X}^{(n)}\toop \bb X$ and consider a sequence of positive numbers

$\epsilon_i$ such that

$\sum_i \epsilon_i < \infty$ . For each

$\epsilon_i$ , we can find a natural number

$n_i'$ such that

$\P(\|{\bb X}^{(n)} -\bb X \|\geq \epsilon_i) < \epsilon_i$ for all

$n>n_i'$ . We can assume without loss of generality that

$n_1' < n_2' < n_3' < \cdots$ (otherwise replace

$n_i'$ with

$\max(n_1',n_2',\ldots,n_i')$ ).

Defining $A_i$ to be the event $\{\|{\bb X}^{(n_i')}-\bb X\|\geq \epsilon_i\}$ , we have $\sum_i \P(A_i)\leq \sum_i \epsilon_i < \infty$ and by the first Borell-Cantelli Lemma (Proposition 6.6.1) we have $\P(A_i \text{ i.o.})=0$ . Since $\lim_{k\to\infty}\epsilon_k=0$ , this implies that for all $\epsilon>0$ , $\P(\{\|{\bb X}^{(n_i')}-\bb X\|\geq \epsilon\} \text{ i.o.})=0$ , which by Proposition 8.2.1 implies that ${\bb X}^{(n_i')}\tooas \bb X$ as $i\to\infty$ . We have thus shown that there exists a subsequence $n_1',n_2',\ldots$ of $1,2,\ldots$ along which convergence with probability 1 occurs.

Considering now an arbitrary sequence $n_1,n_2,\ldots$ of natural numbers, we have ${\bb X}^{(n_i)}\toop \bb X$ as $i\to\infty$ , and repeating the above argument with $n_1,n_2,n_3,\ldots$ replacing $1,2,3,\ldots$ we can find a subsequence $r_1,r_2,r_3,\ldots$ of $n_1,n_2,n_3,\ldots$ along which ${\bb X}^{(r_i)}\tooas \bb X$ as $i\to\infty$ .

To show that converse, we assume that ${\bb X}^{(n)}\not\toop \bb X$ . Then there exists $\epsilon>0$ and $\delta>0$ such that $\P(\|{\bb X}^{(k)}-\bb X\|\geq \epsilon)>\delta$ for infinitely many $k$ , which we denote $n_1,n_2,\ldots$ . This implies that there exists no subsequence of $n_1,n_2,\ldots$ along which ${\bb X}^{(n_i)}\tooas \bb X$ .